Bonus: In a GMAT exam, you will have to attempt 80 questions including an essay question. And you have 3.5 hours to complete the exam.
Compared to other question types on the GMAT, we understand that the GMAT inequalities questions can be slightly trickier. GMAT uses inequalities as a potent weapon to bring down the scores of candidates.
Some of the most insanely challenging GMAT 700-level questions would be reserved for this section on the GMAT. Even moderately difficult GMAT inequalities questions may create havoc when wrong strategies are applied or if you have poor fundamentals.
In fact, we know a lot of GMAT takers who ended up with not-so-great GMAT Quant scores because:
1. They did not understand the basics of GMAT inequalities
2. They did not know how to apply the concepts when faced with inequalities questions on the GMAT
3. They treated them similar to equations (For example, if x/y > 1 they would consider x>y without realizing that the signs of x and y are unknown and if x is negative the analysis would stay flawed!)
4. They hardly made use of the ‘number line’ though they were aware of it (Number line and visualization of a range of solutions are a potent arsenal to tackle GMAT inequalities questions in under 2 minutes
5. They consider values like x/y as a fraction instead of focussing on the signs when it’s an inequality (Don’t worry! We will get into the details soon)
Do you face similar problems?
Do you want to be clear about the concepts in GMAT inequalities before you go ahead and practice questions?
If you just nodded ‘yes’ to both the questions above, you have come to the right place. 😉
Because we are going to answer all the questions you have on GMAT inequalities:
1. What are GMAT inequalities and inequalities signs?
2. What are the basic rules for GMAT inequalities?
3. What are the advanced rules for GMAT inequalities?
4. How to solve GMAT inequalities questions with the Wavy Curve Method?
5. What is the rule for squaring inequalities?
6. What are the points to remember while solving GMAT inequalities questions?
7. BONUS! How to solve inequalities questions on the GMAT? (10 questions with solutions!)
If you have any other questions about inequalities on the GMAT, feel free to drop them as comments below. Our Quant experts will be happy to answer them for you.
1. What are GMAT inequalities and inequalities signs?
Inequalities, just like equations, are mathematical sentences formed by relating two expressions to each other.
But unlike an equation in which an ‘=’ sign joins the two expressions, an inequality is depicted using four other signs. And that’s what we call the GMAT inequalities signs.
For the uninitiated, please get ready to be reminded of your Math classes in school!
Here are the 4 GMAT inequalities signs:
1. > – Greater than
2. < – Lesser than
3. ≥ – Greater than or equal to
4. ≤ – Lesser than or equal to
What do these signs mean when used in an expression, right? Let’s take a look at it.
x > y —-> x is greater than y
x < y —-> x is lesser than y
x ≥ y —-> x is greater than or equal to y
x ≤ y —-> x is lesser than or equal to y
| Inequality Sign | W.r.t variables x & y | Interpretation |
|---|---|---|
| > | x > y | x is greater than y |
| < | x < y | x is lesser than y |
| ≥ | x ≥ y | x is greater than or equal to y |
| ≤ | x ≤ y | x is lesser than or equal to y |
Now that you are familiar with the GMAT inequalities signs and expressions, let’s look at a scenario in which you are given and inequality:
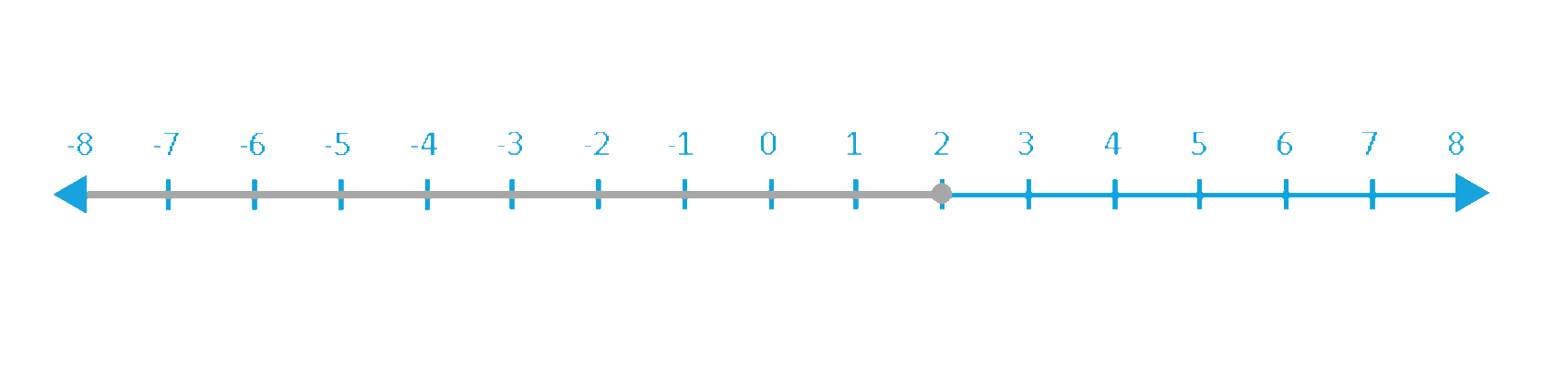
x ≤ 2
How can you understand it better?
The best way to visualize and understand an inequality is by representing it on a number line.
Considering the inequality, x ≤ 2. Here’s how you can represent it on a number line.
Let us consider another example: x > 5
Do you find any difference between the two number lines?
Yes! We are sure you have noticed it.
The first number line has a closed or shaded circle, whereas the second number line has an open or unshaded circle.
Here’s what they mean:
1. A closed (shaded) circle at the endpoint of the shaded portion of the number line indicates that the graph is inclusive of that endpoint, as in the case of inequality signs, ≤ or ≥.
Here’s another example for you:
-3 ≤ x ≤ 4
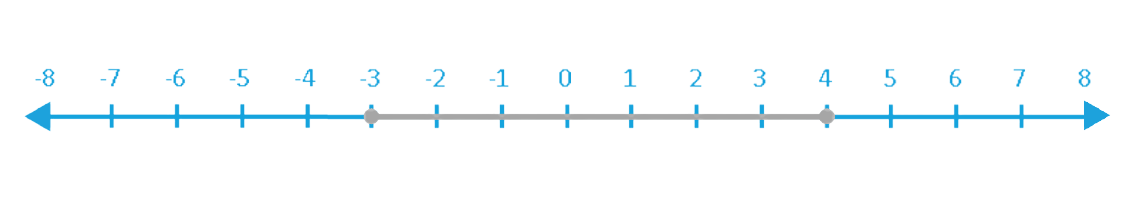
2. An open (unshaded) circle at the endpoint of the shaded portion of the number line indicates that the graph is not inclusive of that endpoint, as in the case of < or >.
Here’s another example for you:
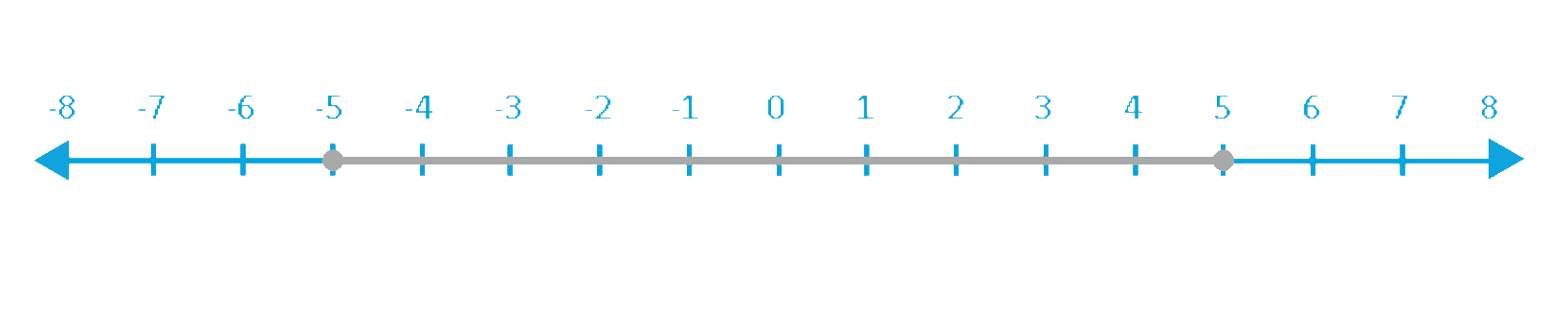
-5 ≤ x < 5
TAKEAWAYS
1. THERE ARE FOUR GMAT INEQUALITIES SIGNS: >, <, ≥, ≤
2. WHEN REPRESENTING AN INEQUALITY ON A NUMBER LINE, YOU CAN USE A CLOSED (SHADED) CIRCLE OR AN OPEN (UNSHADED) CIRCLE DEPENDING ON THE INEQUALITIES EXPRESSION
2. What are the basic rules for GMAT inequalities?
There are two basic rules for GMAT inequalities:
1. Adding or subtracting the same expression to both sides of an inequality does not change the sign of inequality. So, if a < b
a+k < b+k and a-k < b – k (Always True)
In simpler ways of observation, if A has more money than B and 3$ are added to both A and B’s account, A will STILL have more money than B and the greater than sign remains unchanged. The same holds true if 3$ are taken away from each. The ‘greater than’ sign remains the same.
Multiplying or dividing the same positive number to both sides of an inequality does not change the inequality.
2. Multiplying or dividing the same negative number to both sides of an inequality reverses the inequality – this is also called the flip rule of inequalities.
Let us now try and understand these two rules for inequalities using the examples below.
GMAT inequality rule 1
Adding or subtracting the same expression to both sides of an inequality does not change the inequality.
AND
Multiplying or dividing the same positive number to both sides of an inequality does not change the inequality.
If we consider the true inequality,
4 < 8
Adding 2 to both sides 6 < 10 (the inequality sign holds true)
Subtracting 2 from both sides 2 < 6 (the inequality sign holds true)
Multiplying both sides by +2 8 < 16 (the inequality sign holds true)
Dividing both sides by +2 2 < 4 (the inequality sign holds true)
As you can see from the above example, adding, subtracting, multiplying, or dividing both sides of an inequality with the same positive number does not change the inequality.
The inequality sign holds true in all four cases.
We hope that you are clear on this rule of GMAT inequality now. 🙂
GMAT inequality rule 2:
Multiplying or dividing the same negative number to both sides of an inequality, reverses the inequality – this is also called the flip rule of inequalities.
Considering the true inequality we used to explain the first rule here:
4 < 8 Multiplying both sides by -2 -8 > -16 (the inequality sign reverses)
Dividing both sides by -2 -2 > -4 (the inequality sign reverses)
Have any questions?
Now that we are done with the basic rules for GMAT inequalities, we are sure that you will have a few questions in mind. And so, let us take up this opportunity to answer them.
Here are a couple of questions on GMAT inequalities to make you think.
Can we add or subtract a variable on both sides of an inequality?
Yes, because adding or subtracting a variable is the same as adding or subtracting a number.
Can we multiply or divide both sides of an inequality by a variable?
No, we cannot, if we do not know the sign of the number that the variable stands for. The reason is that you would not know whether to flip the inequality sign.
Let us illustrate this with an example:
If x/y > 1, most test-takers make the mistake of deducing that x>y, by multiplying both sides by y. But we haven’t been given any information about the sign of the number that the variable y stands for.
If x = 3 and y = 2 then the above relation x/y > 1 will hold true, and x will be greater than y.
However if x = -3 and y= -2 then the above relation x/y > 1 will again hold true, but x will not be greater than y.
If x/y > 1, the only fact that can definitely be deduced is that both x and y are of the same sign.
GMAT inequalities practice questions – Check if you have got the concepts correct
If a, b, c are non-zero integers and a > bc, then which of the following must be true?
I. a/b > c
II. a/c > b
III. a/bc > 1
Answer options (Make sure you eliminate the wrong answers!)
A. I only
B. II only
C. III only
D. I, II, and III
E. None of these
The million-dollar answer is here
The correct answer option for this GMAT inequalities question is E
Solution
The trap answer here will be D (I, II, and III). The general tendency will be to multiply both sides of the first inequality a/b > c by b to get a > bc, both sides of the second inequality by c to get a > bc, and both sides of the third inequality by bc to get a > bc.
Remember that we can never multiply or divide both sides of an inequality by a variable if the sign of the variable is not known. In this problem, the signs of b and c are not known. The above statements I, II, and III can be true if b and c are both positive. But they will not be true if b and c are negative. Since the question is of a ‘must-be-true’ type, the answer here must be E.
Want to practice a GMAT inequalities question?
Click here to get a question.
Solve: -6x + 4 ≤ -2
Learn how to solve an inequality
Solving an inequality means finding all of its solutions. A ‘solution’ of inequality is a range of values that satisfies the inequality.
Before we begin solving the inequality, let us give you the steps to solve a linear inequation here.
The three steps to solve a linear inequation are as follows:
i. Isolate the variable and always keep the variable positive
ii. Solve using the properties of inequalities. Do not cancel or cross multiply unless you are aware of the signs of the variables involved
iii. Represent the inequality on a number line
If you haven’t solved it yet, do take a look at the solution provided below. 🙂
Coming back to our question,
Solve: -6x + 4 ≤ -2
Solution
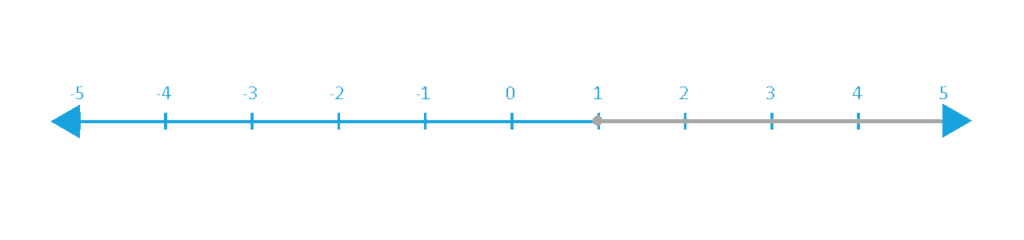
Isolating the variable by subtracting 4 from both sides we get
-6x + 4 -4 <= -2 -4 => -6x ≤ -6
Dividing both sides by -6 and flipping the inequality sign(because we are dividing by a -6 which is < 0), we get x ≥
TAKEAWAYS
1. ADDING OR SUBTRACTING THE SAME EXPRESSION TO BOTH SIDES OF AN INEQUALITY DOES NOT CHANGE THE INEQUALITY
2. MULTIPLYING OR DIVIDING THE SAME NEGATIVE NUMBER TO BOTH SIDES OF AN INEQUALITY, REVERSES THE INEQUALITY – THIS IS ALSO CALLED THE FLIP RULE OF INEQUALITIES
3. What are the advanced rules for GMAT inequalities?
GMAT inequalities can exist in different forms. It need not be just two numbers split by an inequality sign.
You will have fractional inequalities, square root inequalities, quadratic inequalities, like inequalities, max-min inequalities and more.
To solve these inequalities, you need to know what they are and how to approach them. That’s precisely what we will do here. We will look at:
1. Inequalities in fractions
2. Square root inequalities
3. Reciprocal of inequalities
4. Like inequalities
5. Max-Min inequalities
6. Quadratic inequalities
Let’s look at each of them in detail.
1. Inequalities In Fractions
You must be familiar with fractions, right?
But, how do you solve inequalities in fractions?
We use the number line to represent fractions as well. Here’s how.
All proper fractions on the number line can be represented using the range -1 < x < 1. ‘x’ here represents the proper fraction.
All positive proper fractions can be represented using the range 0 < x < 1 where x represents the positive proper fraction
For all proper fractions, (0 < x < 1),
√x > x > x2
If x = ¼ then √x = ½ and x2 = 1/16
Here ½ > ¼> 1/16
GMAT inequalities practice questions – Check if you have got the concepts correct
If x = 0.888, y = √0.888 and z = (0.888)2, which of the following is true?
Answer options (Make sure you eliminate the wrong answers!)
A. x < y < z
B. x < z < y
C. y < x < z
D. z < y < x
E. z < x < y
The million-dollar answer is here
The correct answer option for this GMAT inequalities question is E
Solution
0.888 is a decimal between 0 and 1 = x
√0.888 = √x = y
(0.888)2 = x2 = z
√0.888 > 0.888 > (0.888)2
y > x > z; As we know that for 0<x<1,√x > x > x2
Reversing the inequality we get z < x < y
2. Square root inequalities
Are you familiar with solving square root equations?
If you are, then you might find solving square root inequalities simpler.
Either way, a square root inequality is a mathematical expression that has a square root on at least one part of the expression.
Let’s say, √x+7 ≥ 3. This is an example of a square root inequality.
Here’s another example:
If x2 < a2, then x > -a and x < a, the range of x will be – a < x < a
For example, if x2 < 100 then the values of x that are going to satisfy the inequality are values of x < 10 and values of x > -10.
If x2 > a2, then x > a and x < -a, the range of x will be from (-∞, -a) and (a, ∞)
For example, if x2 > 100 then the values of x that are going to satisfy the inequality are values of x > 10 and values of x < -10.
Solution
If x2 < a2 then the range of x is -a < x < a.
Now x here is replaced by y – 5 and a is replaced by 6 (since 62 = 36).
(y – 5)2 < 36 —-> -6 < y – 5 < 6.
Now adding 5 throughout and isolating the variable y we get,
(y – 5)2 < 36 —-> -6 + 5 < y – 5 + 5 < 6+ 5
(y – 5)2 < 36 —-> -1 < y < 11
3. Reciprocal inequalities
Consider a and b as the two components.
Taking the reciprocal of both a and b can change the direction of the inequality.
The general rule is that when a < b then:
If (1/a ) > (1/b) when a and b are positive.
That is, flip the inequality.
If 2 < 3, then ½ > 1/3
If (1/a) > (1/b) when a and b are negative .
That is, flip the inequality.
If -3 < -2, then 1/-3 > 1/-2
If (1/a) < (1/b) when a is negative and b is positive.
Do not flip the inequality.
If -3 < 2, then 1/-3 < ½
If you do not know the sign of a or b, you cannot take reciprocals.
In summary, if you know the signs of the variables, you should flip the inequality unless a and b have different signs.
GMAT inequalities practice questions – Check if you have got the concepts correct
If 3 ≤ 6/(x+1) ≤ 6, find the range of x.
Solution
Taking the reciprocal of the above range and flipping the inequality sign since the entire inequality is positive
1/3 ≥ (x + 1)/6 ≥ 1/6
Multiplying throughout by 6
2 ≥ (x + 1) ≥ 1
Subtracting 1 from all sides
1 ≥ x ≥ 0 –> 0 ≤ x ≤ 1
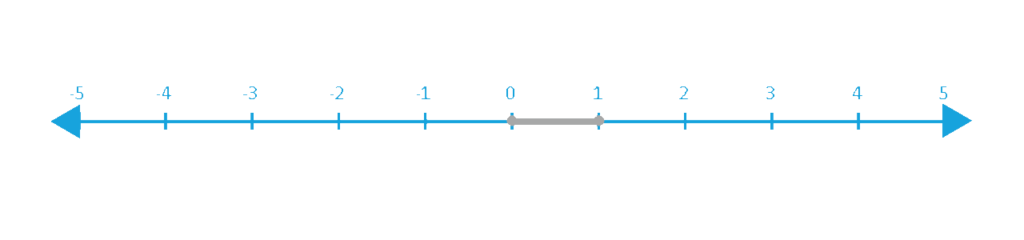
4. Like inequalities
The only mathematical operation you can perform between two sets of inequalities, provided the inequality sign is the same, is addition.
If the signs are not the same then use the properties to flip the inequality sign and then add the two sets of inequalities.
GMAT inequalities practice questions – Check if you have got the concepts correct
If 4a + 2b < n and 4b + 2a > m, then b – a must be:
A. < (m – n)/2
B. ≤ (m – n)/2
C. > (m – n)/2
D. ≥ (m – n)/2
E. ≤ (m + n)/2
The million-dollar answer is here
The correct answer option for this GMAT inequalities question is C
Solution
Given 4a + 2b < n and 4b + 2a > m. We can always add “like” inequalities.
Multiplying the second inequality
4b + 2a > m by -1 we get -4b – 2a < -m.
Now adding the two inequalities
4a + 2b < n and -4b – 2a < -m
4a + 2b < n
-4b – 2a < -m
________________
2a – 2b < n – m
Dividing both sides by 2
a – b < (n – m)/2 Multiplying both sides by -1 b – a > (m – n )/2 (option c)
Grab your free copy of ‘Demystifying GMAT Focus Edition’
5. Min and Max inequalities
What are these minimum and maximum inequalities questions?
On the GMAT, you will come across inequalities questions in which you will have to find the minimum and maximum possible values. For instance, given an inequality expression, you may be asked to find the minimum and maximum values of ‘ab’.
Problems involving optimization: specifically, minimization or maximization problems are a common occurrence on the GMAT. In these problems, you need to focus on the largest and smallest possible values for each of the variables.
This is because some combination of them will usually lead to the largest or smallest possible result.
Let’s understand this better with some examples.
If -7 ≤ x ≤ 6 and -7 ≤ y ≤ 8, what is the maximum possible value for xy?
To find the maximum and minimum possible values for xy, place the inequalities one below the other and make sure the inequality signs are the same. You need to test the extreme values for x and for y to determine which combinations of extreme values will maximize ab.
-7 ≤ x ≤ 6
-7 ≤ y ≤ 8
The four extreme values of xy are 49, 48, -56 and -42. Out of these, the maximum possible value of xy is 49 and the minimum possible value is -56.
Whenever two ranges of inequalities are given in x and y and you need to evaluate the value of x + y, x * y, and x – y then use the max-min concept:
1. Place the two inequality ranges one below the other
2. Make sure the inequality signs are the same in both cases
3. If the signs are not the same, use the properties we have discussed before to make them the same
4. Now add/multiply/subtract both in a straight line and diagonally to get 4 values
5. The greatest value will be “max” and the lowest value will be “min”
Want to solve another question?
Click here to get a question
Is xy < 6 ?
I. x < 3 and -y > -2
II. y2 < 100 , 1/2 < x < 2/3
Learn how to solve an inequality
Evaluating Statement 1 individually
x < 3 and y < 2 (Multiplying both sides by -1 and flipping the inequality sign)
Now If x = 2 and y = 1 then xy = 2 which gives a YES
If x = -3 and y = -2 then xy = 6 which gives a NO
Statement 1 is Insufficient
Evaluating Statement 2 individually
y2 < 100 —> -10 < y < 10 ;
1/2 < x < 2/3.
Placing the ranges of x and y one below the other and using the max-min concept we have the maximum value of xy to be 20/3 which gives a YES and the minimum value of xy to be -20/3 which gives a NO.
Statement 2 is Insufficient
Combining Statements 1 and 2,
Now the range of x is still going to be 1/2 < x < 2/3 but the range of y is going to be – 10 < y < 2 (Since y < 2 from statement 1)
Now using the max-min concept for the above ranges of x and y, we have the maximum value of xy to be 4/3 and the minimum value of xy to be -20/3. All possible values of xy here are less than 6 which gives a definite YES.
Now let us take a look at Quadratic inequalities.
6. Quadratic inequalities
In simple terms, quadratic inequalities are mathematical expressions that are similar to quadratic equations but use inequality signs instead of an ‘=’ sign.
Let’s look at an example,
3×2 – 7x + 4 ≤ 0
Factorizing the above quadratic inequation
3×2 – 7x + 4 ≤ 0 —> 3×2 – 3x – 4x + 4 ≤ 0 —> 3x(x – 1) – 4(x – 1) ≤ 0 —> (3x – 4)(x – 1) ≤ 0
We get 1 and 4/3 as critical points. We place them on the number line.

Since the number line is divided into three regions, now we can get 3 ranges of x:
i) x < 1 (all values of x when substituted in (3x – 4)(x – 1) makes the product positive)
ii) 1 ≤ x ≤ 4/3 (all values of x when substituted in (3x – 4)(x – 1) makes the product negative)
iii) x > 4/3 (all values of x when substituted in (3x – 4)(x – 1) makes the product positive)
At this point we should understand that for the inequality (3x-4)(x-1) ≤ 0 to hold true, exactly one of (3x-4) and (x-1) should be negative and the other one should be positive. Let’s examine 3 possible ranges one by one.
i) If x > 4/3, obviously both the factors i.e. (3x-4) and (x-1) will be positive and in that case, inequality would not hold true. So this cannot be the range of x.
ii) If x is between 1 and 4/3 both inclusive, (3x-4) will be negative or equal to zero and (x-1) will be positive or equal to zero. Hence with this range, the inequality holds true. Correct.
iii) If x < 1, both (3x-4) and (x-1) will be negative hence inequality will not hold true.
So the range of x that satisfies the inequality 3×2 – 7x + 4 ≤ 0 is 1 ≤ x ≤ 4/3.
The steps to solve quadratic inequation are as follows:
i. Isolate the variable and always keep the variable positive.
ii. Maintain the Inequation in the form ax2 + bx + c > 0 or < 0.
iii. Obtain the factors of Inequation.
iv. Place them on the number line. The number line will get divided into three regions.
v. Mark the rightmost region with + sign, the next region with a – sign and the third region with a + sign (alternating + and – starting from the rightmost region).
vi. If the Inequation is of the form ax2 + bx + c < 0, the region having the – sign will be the solution of the given quadratic inequality.
In other words,
If the inequality is ax2 + bx + c < 0, the range of solutions will be the part in the middle i.e. Smallest Root < x < Biggest Root
For example if (a-3)(a-6) < 0 ,
the range for a would be 3 < a < 6
vii. If the Inequation is of the form ax2 + bx + c > 0, the region having the + sign will be the solution of the given quadratic inequality.
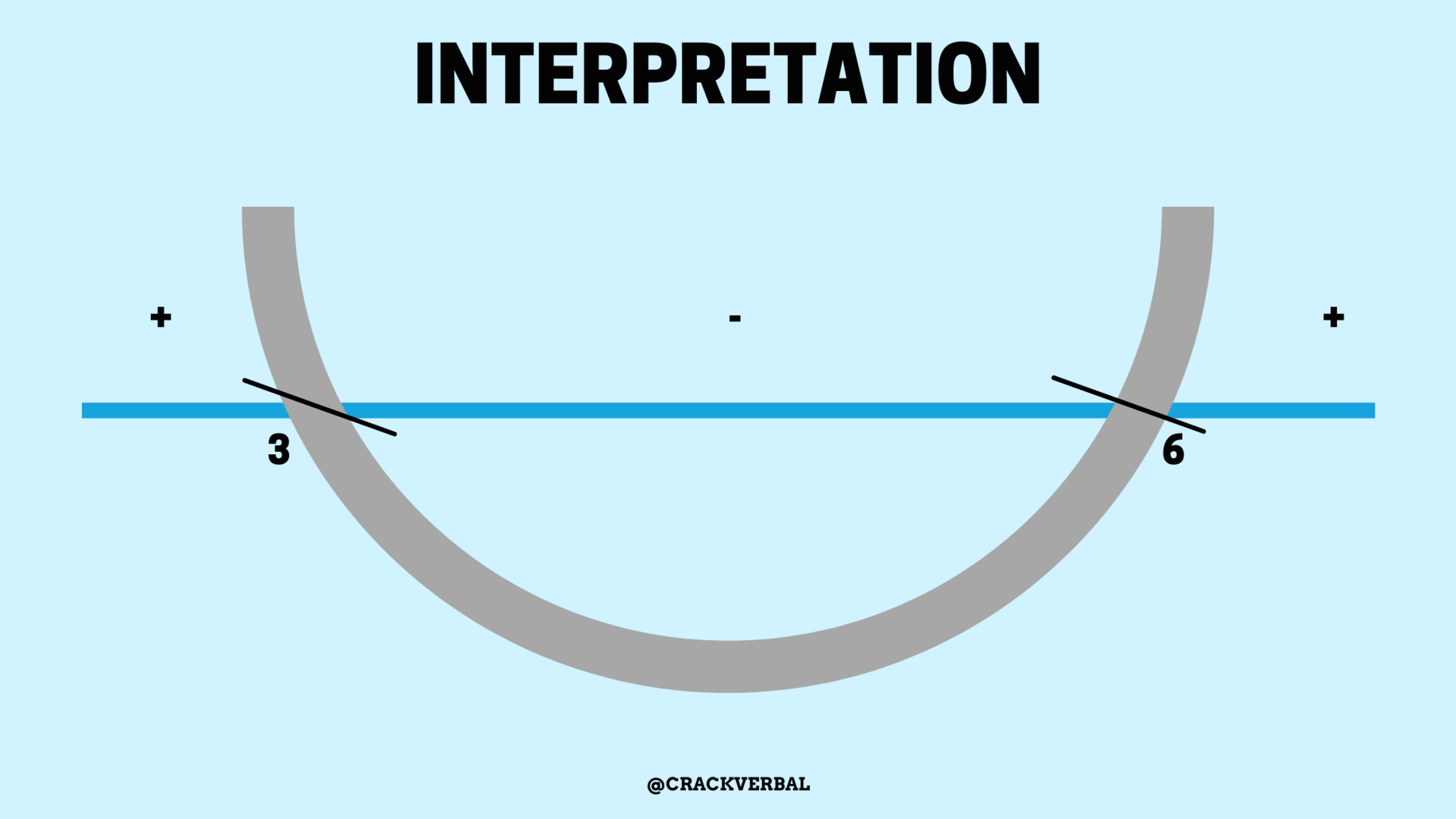
In other words,
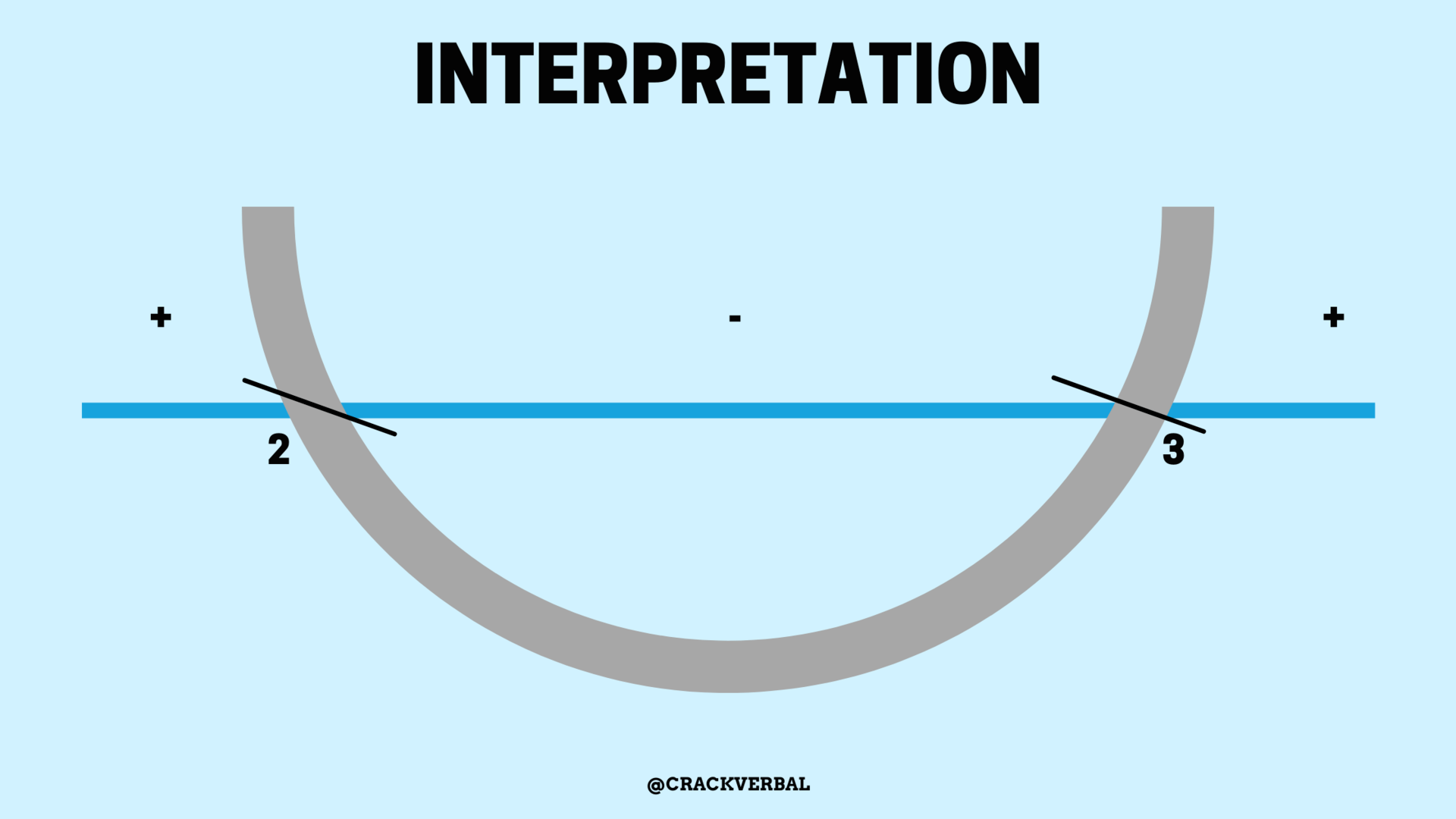
If the inequality is ax2 + bx + c > 0, the range of solutions will be the right most part and the left most part i.e. x> Biggest root OR x< Smallest Root
For example,
x2 – 5x+6 > 0
=>(x-3)(x-2) >0
x>3,x<2
4. How to solve GMAT inequalities questions with the Wavy Curve Method?
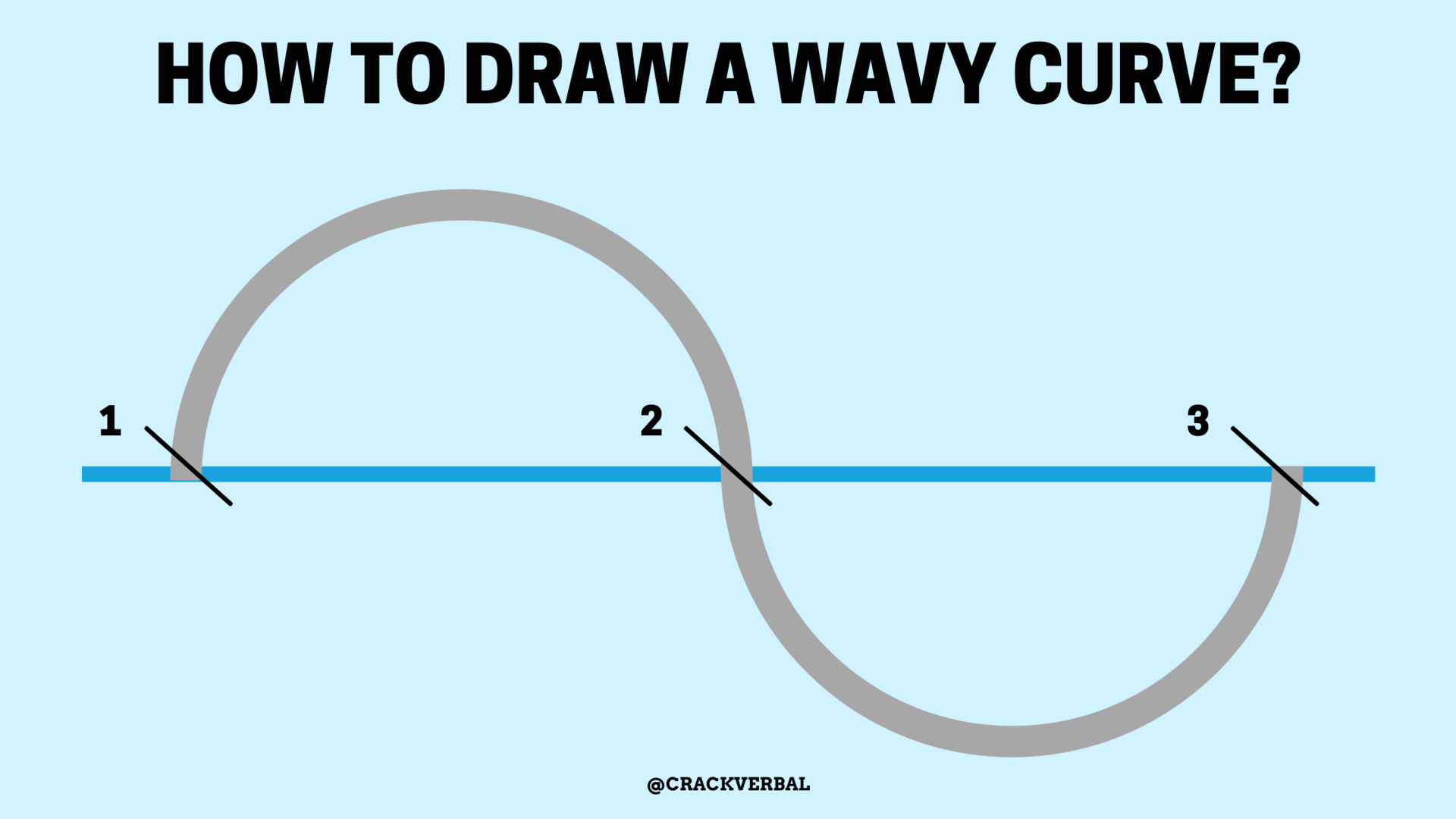
You have heard of the ‘Wavy Curve’ method but don’t know how to solve GMAT inequalities questions using it?
Here’s how you can use the Wavy Curve method to solve GMAT inequalities questions:
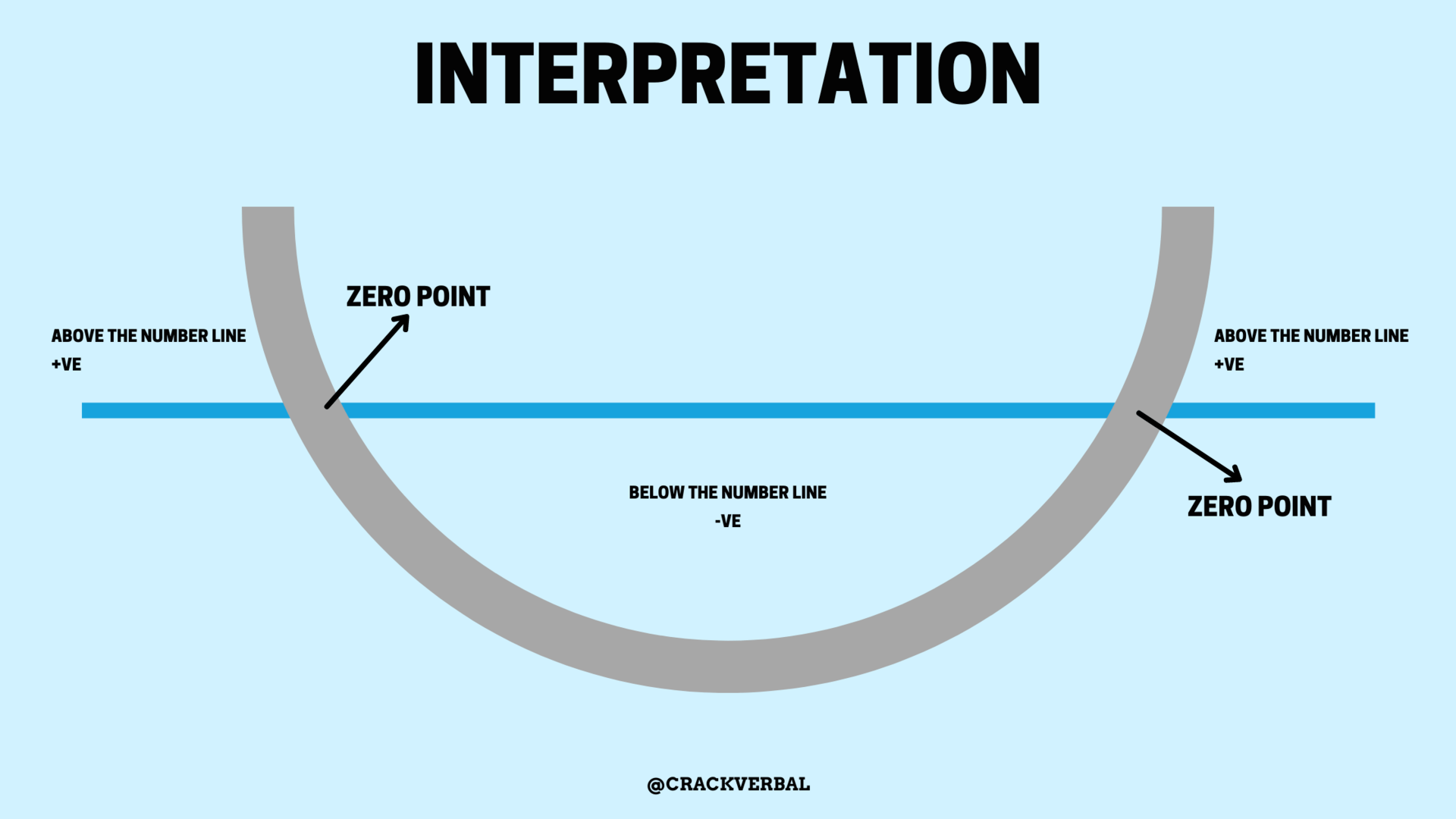
i. First draw a horizontal line – It would be a Number Line to identify the range of the variable in question
ii. Represent “zero points” on the line: Note the values at which at least one of the factor terms in the expression become zero
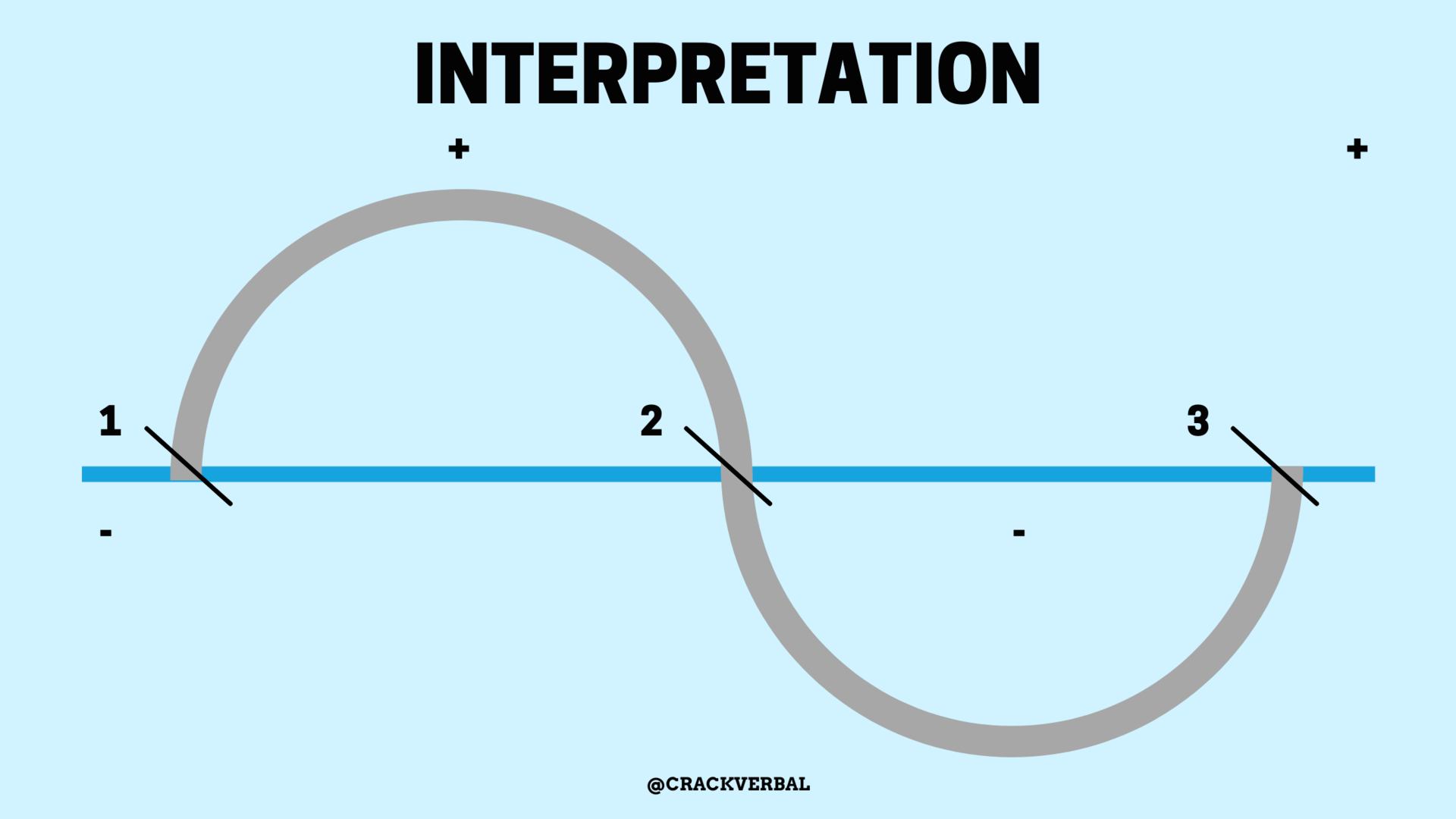
For example, if (x-3) as a term in an inequality is 0, then mark x-3 as 0. The same occurs at (x-1) and (x-2) as 0
iii. Start creating the wavy curve from the top right portion
iv. If the term has odd power, the wavy curve passes through the respective root/zero point
v. If the term has an even power, the wavy curve bounces off the respective zero point
NOTE
1. ON THE REGION(S) ABOVE THE NUMBER LINE, THE VALUE OF EXPRESSION SHALL BE POSITIVE
2. ON THE INTERSECTION POINTS, VALUE OF EXPRESSION EQUALS ZERO
3. ON THE REGION(S) BELOW THE NUMBER LINE, THE VALUE OF EXPRESSION SHALL BE NEGATIVE
How to deal with fractions using a wavy curve?
Let’s take a question to understand this:
Solution
It is important here to point out that the question stem can be rephrased as
Is (x+1)(x-3) < 0? (After multiplying(x-3) in both Numerator and Denominator)
The critical points would be -1 and 3
Using the wavy curve approach we can establish the range of x as -1 < x <3
In such a case, you have to be slightly careful and observe that with (x-3) in the original question stem as the denominator implies we cannot consider any case where the denominator is 0. In other words, we cannot include x=3 and hence the value of x=3 would stand excluded.
The range would then be -1 < x < 3(If the < in the question was replaced by a ≤)
Question: Will the above procedure hold good even for a cubic or a fourth-degree equation?
Answer: YES. For a cubic inequality, we get 3 critical points which when plotted on the number line divides the number line into 4 regions. Mark the rightmost region as +ve and alternate the sign as shown below
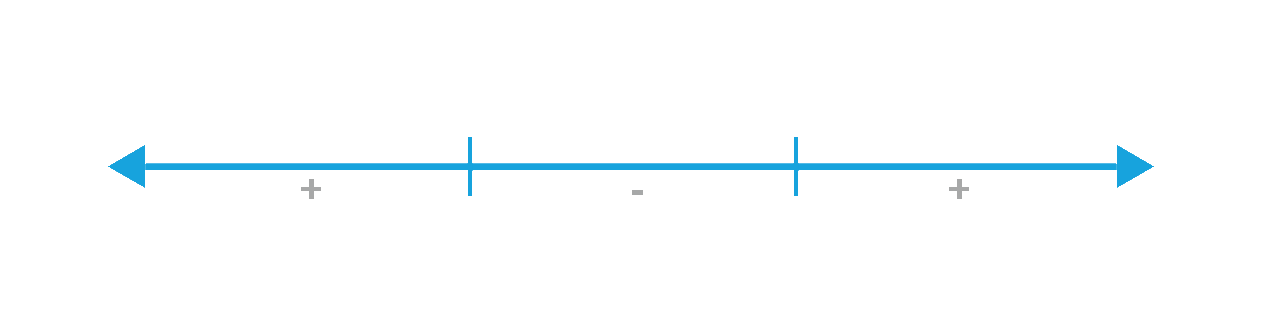
For example if,(x-1)(x-2)(x-3) > 0 and we want to find the range for x in this cubic inequality we shall obtain 1< x < 2 or x > 3 as the solution range
Still not sure how to approach GMAT inequalities questions?
Feel free to drop your query in the comments section below. Our Quant experts will be happy to help you. 🙂
GMAT inequalities practice questions – Check if you have got the concepts correct
How many of the integers that satisfy the inequality (x + 2) (x + 3) (x – 2) >=0 are less than 5?
A. 1
B. 2
C. 3
D. 4
E. 5
The million-dollar answer is here
The correct answer option for this GMAT inequalities question is E
Solution
The 3 critical points here are at -2, -3 and 2. Now using the concept of quadratic inequalities and plotting the critical points on the number line we get,
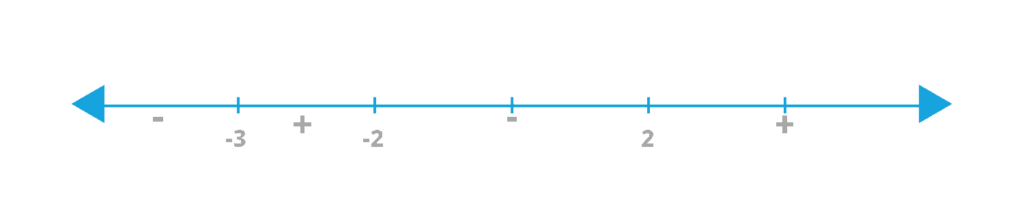
Now since the right-hand side is >= 0 we need to consider the positive regions of the number line. The range of x where the given inequality expression is positive is x >= 2 and -3<= x < = -2. From the range of x, the integer values less than 5 are 2, 3, 4, -3 and -2.
Feel that you are familiar with different types of GMAT inequalities questions now?
Is yes, that is great! If not, drop your queries so that we can help you out.
While we discussed different inequalities questions on the GMAT above, we did leave out one. That is squaring inequalities.
We will be taking an in-depth look at them because we have seen that a lot of GMAT aspirants have doubts about squaring inequalities.
We will simplify it for you
5. What is the rule for squaring inequalities?
Can you square both sides of an inequality?
We cannot square both sides of inequality unless we know the signs of both sides of the inequality.
IF BOTH SIDES ARE KNOWN TO BE NEGATIVE, THEN FLIP THE INEQUALITY SIGN WHEN YOU SQUARE
For instance, if a < -4, then the left-hand side must be negative. Since both sides are negative, you can square both sides and reverse the inequality sign: a2 > 16. However, if a > -4, then you cannot square both sides, because it is unclear whether the left side is positive or negative. If a is negative then a2 < 16, but if x is positive then x2 could be either greater than 9 or less than 9.
If both sides are known to be positive, do not flip the inequality sign when you square.
For instance, if a > 4, then the left side must be positive; since both sides are positive you can square both sides to yield a2 > 16. However, if a < 4 then you cannot square both sides, because it is unclear whether the left side is positive or negative.
If one side is positive and one side is negative then you cannot square.
For instance, if you know that a < b, a is negative, and b is positive, you cannot make any determination about x2 vs. y2.
If for example, x = -2 and y = 2, then x2 = y2.
If x = -2 and y = 3, then x2 < y2.
If x = -2 and y = 1, then x2 > y2.
Note: If one side of the inequality is negative and the other side is positive, then squaring is probably not warranted.
If signs are unclear, then you cannot square the inequalities.
Put simply, we would not know whether to flip the sign of the inequality once you have squared it.
For example if x>- 3, x is not definitely positive. It can be negative or 0. If x = 0, x2 = 0. In this case, 0 < x2 < infinity.
The same can be observed for x< 3 where the range is 0<=x2 < infinity.
6. What are the points to remember while solving GMAT inequalities questions?
You know the inequality signs. We have also given you an understanding of GMAT inequalities, the basic and advanced rules for GMAT inequalities as well. Now that you have an idea of how to solve different types of GMAT inequalities questions, here are a few points you need to keep in mind.
You can try to remember these seven points when you are using the properties of inequalities to simplify complex problem solving and data sufficiency questions in GMAT Quant inequality problems:
i. Add or subtract any quantity on both sides of the inequality without changing the inequality sign.
ii. Multiply or divide by a positive value without changing the inequality sign.
iii. Square both sides only when the quantities are both positive.
iv. When multiplying and dividing by a negative number always flip the inequality sign.
v. Never multiply or divide both quantities by a variable if the sign of the variable is unknown.
vi. If the sign of the variable is always positive then it is possible to multiply or divide both quantities by the positive variable (for e.g. x2, since x2 is always positive).
vii. The only mathematical operation that you can perform between two sets of inequalities is addition. Never subtract, multiply or divide.
7. BONUS! How to solve inequalities questions on the GMAT?
Here’s the bonus section for you!
As promised, we will be giving you 12 GMAT inequalities questions that you can practice.
What if you are unsure about the answer?
Worst case scenario, what if you cannot solve the inequalities questions?
No worries. All you have to do is click on the ‘Solution’ tab under each question to cross-check your answer and to find the solution.
So, here are the 12 GMAT inequalities questions for you:
Q1. Amy had a Maths test and found that a particular question read ,”which of the following inequalities must be true if 0 < a < 1”?
I. a5 < a3
II. a5 +a 4 < a2 + a3
III. a4−a5<a2−a3
A. I only
B. II only
C. I & II only
D. I, II and III
E. None
Check out the answer and the solution here!
The correct answer option for this GMAT inequality question is D
Solution
0 < a< 1, then a > a2> a3> a4 > a5 …
I. a5 < a3 (True)
II. a5 +a 4 < a2 + a3. Each term on the left hand side is less than each term on the right hand side, thus LHS < RHS and hence true.
III. a4−a5<a2−a3 =>a4(1−a)<a2(1−a)
Since 0 < a < 1, then 1 – a > 0, so we can reduce by it: a4
Q2. If 1 < a< b < c, which of the following has the greatest value?
A. c(a+ 1)
B. c(b + 1)
C. a(b+ c)
D. b(a + c)
E. c(a + b)
Check out the answer and the solution here!
The correct answer option for this GMAT inequality question is E
Solution
Plug values a=2,b=3,c=4 , which satisfies the condition 1<a<b<c
If we use this values in the answer options
A. c(a + 1) = 4(3) = 12
B. c(b + 1) = 4(4) = 16
C. a(b + c) = 2(7) = 14
D. b(a + c) = 3(6) = 18
E. c(a + b) = 4(5) = 20
Q3. Jane was counting her numbers and there were x integers that she counted. How many integers x are there so that 1< 5x +5 < 25?
A.1
B.2
C.3
D.4
E.5
Check out the answer and the solution here!
The correct answer option for this GMAT inequalities question is D
Solution
1<5x+5<25 –> subtract 5 from each part: −4<5x<20 –> Divide by 5 each part=>−4/5<x<4. In this range there are 4 integers: 0, 1, 2, and 3
Q4. If it is observed that 5|5-s|=3, what is the sum of all the possible values of s?
A. 13
B. 10
C. 8
D. 7
E. 6
Check out the answer and the solution here!
The correct answer option for this GMAT inequalities question is B
Solution
5 * |5-s| = 3
=> |s-5| = 3/5
=> s is at a distance of 3/5 from 5.
=>one value will be 3/5 more than 5 and the other value will be 3/5 less than 5.
If we add them up, the excess of 3/5 will cancel off with the deficit of 3/5 to give you just two 5s i.e. a total of 10
Q5. If a and b are integers, is a > b ?
(1) a + b > 0
(2) b^a < 0
Check out the answer and the solution here!
The correct answer option for this GMAT inequalities question is C
Solution
(1) a + b > 0. Given that the sum of two numbers is greater than zero, but we cannot determine which one is greater. Insufficient.
(2) b ^a< 0. This statement implies that b is a negative number. Now, if b=-1 and a=1, then a>b BUT if b=-1 and a=-1, then a=b Insufficient.
(1)+(2)
From (2) we have that b is a negative number
=> -b is a positive number.
Therefore from (1) we have that a> -b = positive,
=> a is a positive number. So, we have that a=positive >b=negative.(Sufficient)
Q6. Is p>q?
(1) 6p>5q
(2) pq<0
Check out the answer and the solution here!
The correct answer option for this GMAT inequalities question is C
Solution
Statement 1: 6p>5q
If p=1 and q=1 the answer to the question stem is NO.If p=3 and q=2 then answer to question stem is YES. (Insufficient)
Statement 2:- pq<0 both are of opposite sign but we don’t know which one is greater (Insufficient)
Combining both ,we have either of p or q negative.Since 6p>5q, p is positive and q is negative, p>q (Sufficient)
Q7. If 6/a(a+1)>1, which of the following could the value of a?
A. -3.5
B. -2.5
C. 2.5
D. 3.5
E. 4.5
Check out the answer and the solution here!
The correct answer option for this GMAT inequalities question is B
Solution
6/(product) > 1
=>Denominator must be LESS than 6.
=> 6/(something less than 6) will be > 1.
=>We’re looking for a product that’s less than 6.
We’re looking for a value for “a “that’s relatively close to 0,
Let’s start with options B and C.
B: X = -2.5
Denominator = (-2.5)(-1.5)
C: X = 2.5
Denominator = (2.5)(3.5)
Since the negative signs will cancel out in Answer B, you don’t have to do the math to see that Answer B is smaller. Since there’s only one answer that will satisfy the condition, it has to be B.
Q8. If x (x + y)≠0 and x>0
Is 1/ (x +y) < (1/x ) +y?
(1) x+ y>0
(2) y>0
Check out the answer and the solution here!
The correct answer option for this GMAT inequalities question is B
Solution
(1) x +y>0
Since x+y>0 & x>0, then x(x+y)>0
If y>0, then -y/x(x+y)<0<y but if y≤0
then –y/x(x+y)≥0≥y (Insufficient)
(2) y >0 since x>0 & y>0,
then –y/x(x +y)<0<y (Sufficient)
Q9. If it is true that a > -2 and a < 7, which of the following must be true?
A. a > 2
B. a > -7
C. a< 2
D. -7 < a < 2
E. None of the above
Check out the answer and the solution here!
The correct answer option for this GMAT inequalities question is B
Solution
Given: -2<x<7.
Now, any x from this true range is more than -7, so x>-7 must be true.(option b)
Q10. On the number line, if m<n, if p is halfway between m and n, and if q is halfway between p and m then what is the value of (n-q) /(q-m) ?
A. 1/4
B. 1/3
C. 4/3
D. 3
E. 4
Check out the answer and the solution here!
The correct answer option for this GMAT inequalities question is D
Solution
Let m=0 and n=4 –> p is halfway between m and n
=>p=2
q is halfway between p=2 and m=0
=>q=1
(n-q) /(q-m)
=(4-1)/(1-0)=3
Now that we have given you all the details on how to solve GMAT inequalities questions, through this guide, you will now be able to analyze the traps, plug in values, and solve them.
If you still have any questions regarding the Quant topic, please drop them in the ‘Comments Section’ below. Our experts will definitely get back to you.
And if you need help with improving your GMAT Quant score, you can enroll in our GMAT Advanced Course to learn all the strategies to tackle Quant questions on the exam.
You can click on the image below to know more details on the course offerings we have and to join us!


