Are you wondering, why an entire blog post on Inequalities?
Well, as you may have already found out, compared to other question types on the GRE, inequality questions are an especially slippery slope! They have sent many a test-taker tumbling down on the path to not-so-great Quant scores.
By the time you finish reading this post, you will know all that you need to make sure that this does not happen to you!
So, without further ado, let us examine some must-know inequality concepts and strategies that will help us navigate these tricky questions with limited information .
We’ll first start with the fundamental concept of inequalities, followed by basic properties and then move on to explore the complexities involved with some additional properties. Finally we will summarize the key takeaways with a list of points to keep in mind while using inequalities in problem-solving and data sufficiency questions.
1. What are Inequalities?
Equations and inequalities are both mathematical sentences formed by relating two expressions to each other.
In an equation, the two expressions are deemed equal which is shown by the symbol =.
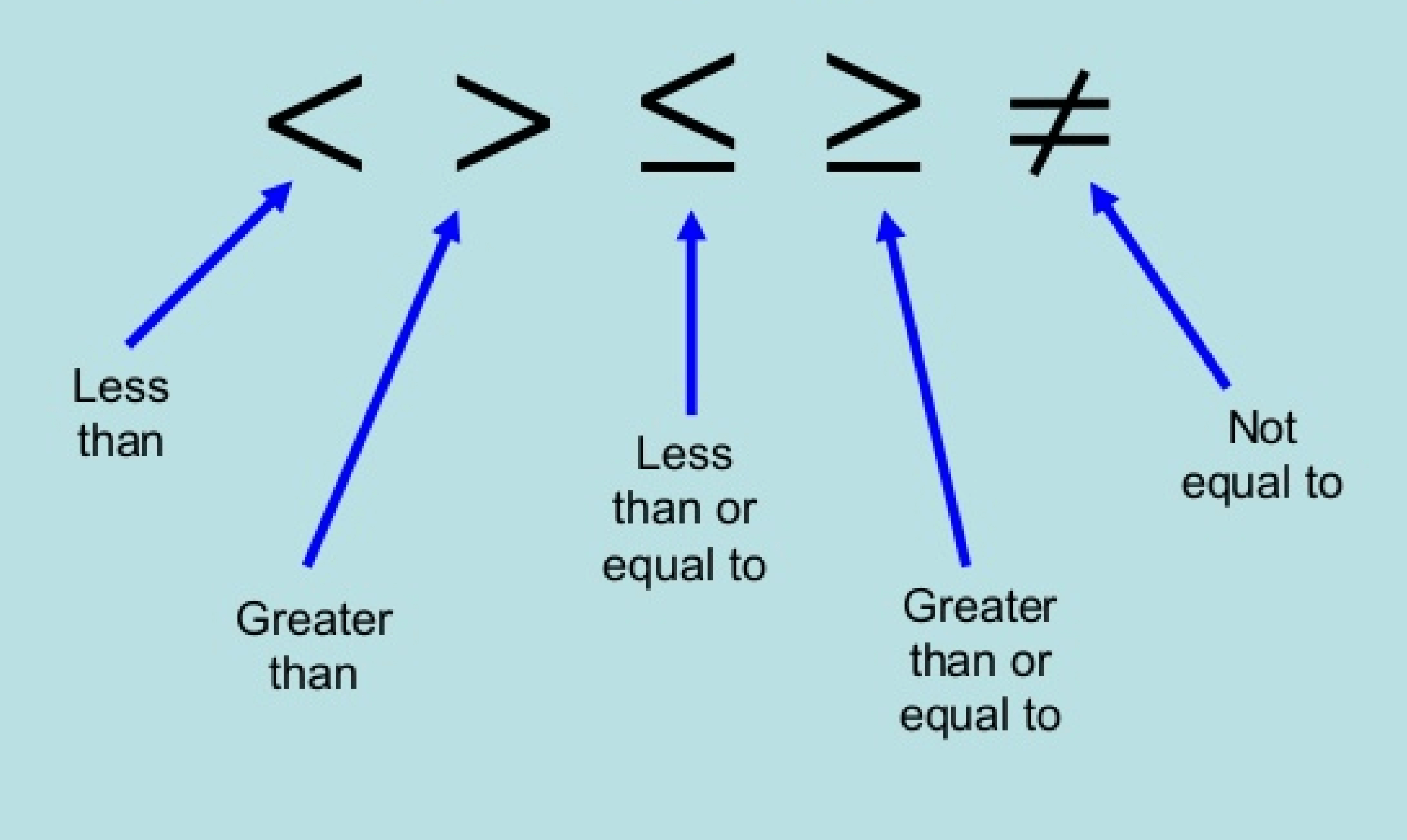
Where as in an inequality, the two expressions are not necessarily equal – this is indicated by the symbols: >, <, ≤ or ≥. x > y —-> x is greater than y
x ≥ y —-> x is greater than or equal to y
x < y —-> x is less than y
x ≤ y —-> x is less than or equal to y
Inequalities on a Number line
Number lines, such as those shown below, are an excellent way to visualize exactly what a given inequality means. A closed (shaded) circle at the endpoint of the shaded portion of the number line indicates that the graph is inclusive of that endpoint, as in the case of ≤ or ≥.

An open (unshaded) circle at the endpoint of the shaded portion of the number line indicates that the graph is not inclusive of that endpoint, as in the case of < or >

2. Basic Properties
There are 2 basic properties of inequalities which we can quickly prove using the example below.
Property 1:
If we consider the true inequality
4 < 8
Adding 2 to both sides 6 < 10 (the inequality sign holds true)
Subtracting 2 from both sides 2 < 6 (the inequality sign holds true)
Multiplying both sides by +2 8 < 16 (the inequality sign holds true)
Dividing both sides by +2 2 < 4 (the inequality sign holds true)
Adding or subtracting the same expression to both sides of an inequality does not change the inequality.
Multiplying or dividing the same positive number to both sides of an inequality does not change the inequality.
Property 2:
Again considering the true inequality
4 < 8 Multiplying both sides by -2 -8 > -16 (the inequality sign reverses)
Dividing both sides by -2 -2 > -4 (the inequality sign reverses)
Multiplying or dividing the same negative number to both sides of an inequality reverses the inequality – this is also called the flip rule of inequalities.
A little Q & A anyone?
Now that we are done with the basic properties of inequalities, here are a couple of questions to make you think.
Question: Can we add or subtract a variable on both sides of an inequality?
Answer: Yes, because adding or subtracting a variable is the same as adding or subtracting a number.
Question: Can we multiply or divide both sides of an inequality by a variable?
Answer: No, we cannot, if we do not know the sign of the number that the variable stands for. The reason is that you would not know whether to flip the inequality sign.
Let us illustrate this with an example –
If x/y > 1, most test-takers make the mistake of deducing that x>y, by multiplying both sides by y. But we haven’t been given any information about the sign of the number that the variable y stands for.
If x = 3 and y = 2 then the above relation x/y > 1 will hold true, and x will be greater than y.
However if x = -3 and y= -2 then the above relation x/y > 1 will again hold true, but x will not be greater than y.
If x/y > 1, the only fact that can definitely be deduced is that both x and y are of the same sign .
Example 1:
Question: If a, b, c are non zero integers and a > bc, then which of the following must be true :
I. a/b > c
II. a/c > b
III. a/bc > 1
A. I only
B. II only
C. III only
D. I, II and III
E. None of these
Solution:
Now the trap answer here will be D (I, II and III). The general tendency will be to multiply both sides of the first inequality a/b > c by b to get a > bc, both sides of the second inequality by c to get a > bc and both sides of the third inequality by bc to get a > bc.
Remember that we can never multiply or divide both sides of an inequality by a variable if the sign of the variable is not known. In this problem the signs of b and c are not known. The above statements I, II and III can be true, if b and c are both positive. But they will not be true if b and c are negative. Since the question is of a ‘must-be-true’ type, the answer here must be E.
Example 2:
Solve: -6x + 4 ≤ -2
Solving an inequality means finding all of its solutions. A ‘solution’ of an inequality is a number which when substituted for the variable satisfies the inequality
The steps to solve a linear inequation are as follows:
- Isolate the variable and always keep the variable positive
- Solve using the properties of inequalities
- Represent the inequality on a number line
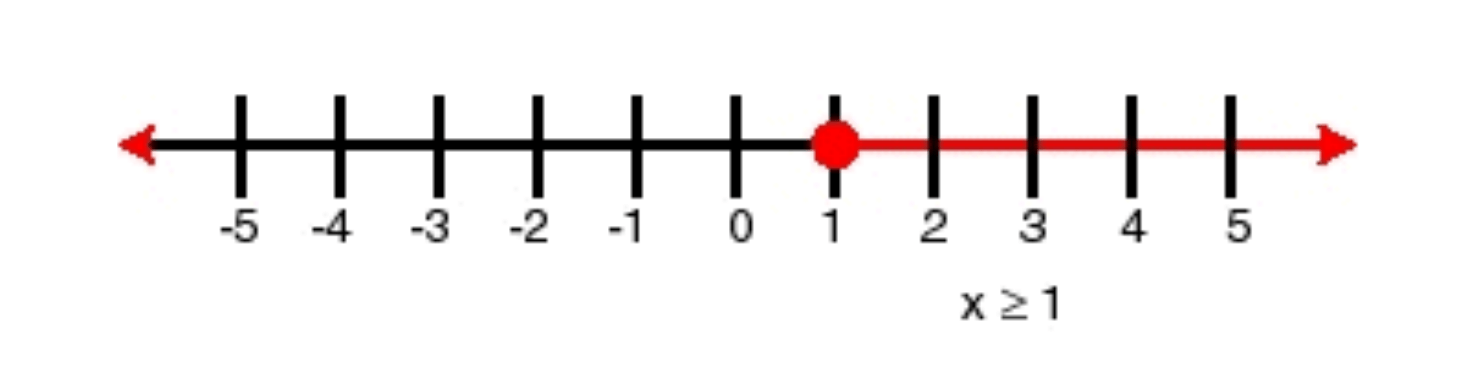
Isolating the variable by subtracting 4 from both sides we get -6x ≤ -6
Dividing both sides by -6 and flipping the inequality sign we get x ≥ 1
3. Advanced Concepts
Well, so far, we saw how the basic operations are applied to inequalities.
It is now time to delve into more complex properties of inequalities, dealing with :
C) Square Root Inequalities
A) Inequalities in Fractions
All proper fractions on the number line can be represented using the range -1 < x < 1 where x represents the proper fraction
All positive proper fractions can be represented using the range 0 < x < 1 where x represents the positive proper fraction
For all proper fractions (0 < x < 1), √x > x > x2
If x = ¼ then √x = ½ and x^2 = 1/16
Clearly here ½ > ¼> 1/16
Example:
If x = 0.888, y = √0.888 and z = (0.888)^2 which of the following is true
A. x < y < z
B. x < z < y
C. y < x < z
D. z < y < x
E. z < x < y
Solution:
Since 0.888 is a fraction,
√0.888 0.888 > (0.888)^2
y > x > z
Reversing the inequality we get z < x < y
Answer: E
B) Squaring Inequalities
We cannot square both sides of an inequality unless we know the signs of both sides of the inequality.
If both sides are known to be negative then flip the inequality sign when you square.
For instance, if a < -4, then the left hand side must be negative. Since both sides are negative, you can square both sides and reverse the inequality sign : a^2 > 16. However, if a > -4, then you cannot square both sides, because it is unclear whether the left side is positive or negative. If a is negative then a^2 < 16, but if x is positive then x^2 could be either greater than 9 or less than 9.
If both sides are known to be positive, do not flip the inequality sign when you square.
For instance, if a > 4, then the left side must be positive; since both sides are positive you can square both sides to yield a^2 > 16. However if a < 4 then you cannot square both sides, because it is unclear whether the left side is positive or negative.
If one side is positive and one side is negative then you cannot square.
For instance, if you know that a < b, a is negative, and b is positive, you cannot make any determination about x^2 vs. y^2.
If for example, x = -2 and y = 2, then x^2 = y^2.
If x = -2 and y = 3, then x^2 < y^2. If x = -2 and y = 1, then x^2 > y^2.
It should be noted that if one side of the inequality is negative and the other side is positive, then squaring is probably not warranted.
If signs are unclear, then you cannot square.
Put simply, we would not know whether to flip the sign of the inequality once you have squared it.
D) Reciprocal Inequalities
Taking the reciprocal of both a and b can change the direction of the inequality.
The general rule is that when a < b then: • (1/a ) > (1/b). When a and b are positive , flip the inequality.
Example: If 2 < 3, then ½ > 1/3
• (1/a) > (1/b). When a and b are negative , flip the inequality.
Example: If -3 < -2, then 1/ -3 > 1/ -2
• For (1/a) < (1/b). When a is negative and b is positive , do not flip the inequality.
Example: If -3 < 2, then 1/ -3 < 1/2 • If you do not know the sign of a or b you cannot take reciprocals. In summary, if you know the signs of the variables, you should flip the inequality unless a and b have different signs.
Example: If 3 ? 6/ (x+1) ? 6, find the range of x
Taking the reciprocal of the above range and flipping the inequality sign since the entire inequality is positive 1/3 ≥ (x + 1)/6 ≥ 1/6 Multiplying throughout by 6 2 ≥ (x + 1) ≥ 1 Subtracting 1 from all sides 1 ≥ x ≥ 0 –> 0 ≤ x ≤ 1
E) Like Inequalities
The only mathematical operation you can perform between two sets of inequalities, provided the inequality sign is the same, is addition.
If the signs are not the same then use the properties to flip the inequality sign and then add the two sets of inequalities.
Example:
If 4a + 2b < n and 4b + 2a > m, then b – a must be
A. < (m – n)/2 B. ≤ (m – n)/2 C. > (m – n)/2
D. ≥ (m – n)/2
E. ≤ (m + n)/2
Given 4a + 2b < n and 4b + 2a > m. We can always add like inequalities.
Multiplying the second inequality
4b + 2a > m by -1 we get -4b – 2a < -m.
Now adding the two inequalities
4a + 2b < n and -4b – 2a < -m
4a + 2b < n
-4b – 2a < -m
________________
2a – 2b < n – m
Dividing both sides by 2
a – b < (n – m)/2
Multiplying both sides by -1
b – a > (m – n )/2
Answer: C
F) Min and Max Inequalities
Problems involving optimization: specifically, minimization or maximization problems are a common occurrence on the GRE .
In these problems, you need to focus on the largest and smallest possible values for each of the variables.
This is because some combination of them will usually lead to the largest or smallest possible result.
Read on to learn from an example.
Example 1:
If -7 ≤ x ≤ 6 and -7 ≤ y ≤ 8, what is the maximum possible value for xy?
To find the maximum and minimum possible values for xy, place the inequalities one below the other and make sure the inequality signs are the same. You need to test the extreme values for x and for y to determine which combinations of extreme values will maximize ab.
-7 ≤ x ≤ 6
-7 ≤ y ≤ 8
The four extreme values of xy are 49, 48, -56 and -42. Out of these the maximum possible value of xy is 49 and the minimum possible value is -56.
Whenever two ranges of inequalities are given in x and y and you need to evaluate the value of x + y , x * y, and x – y then use the max-min concept
1. Place the two inequality ranges one below the other
2. Make sure the inequality signs are the same in both cases
3. If the signs are not the same use the properties we have discussed before to make them the same
4. Now add/multiply/subtract both in a straight line and diagonally to get 4 values
5. The greatest value will be max and the lowest value will be min
1/2 < x < 2/3 , and y^2 < 100
Quantity A Quantity B
xy 6
Since y^2 < 100 —> -10 < y < 10
Now placing the two ranges one below the other and finding out the extreme values of xy
1/2 < x < 2/3
-10 < y < 10
The four extreme values of xy here are -5, -20/3 , 5, 20/3. Out of these the maximum value of xy is 20/3 and the minimum value of xy is -20/3. Now since Quantity A can take values from -20/3 to 20/3 a definite relationship cannot be determined with Quantity B.
Answer: D
G) Quadratic Inequalities
3x^2 – 7x + 4 ≤ 0
Factorizing the above quadratic inequation
3x^2 – 7x + 4 ≤ 0 —> 3x^2 – 3x – 4x + 4 ≤ 0 —> 3x(x – 1) – 4(x – 1) ≤ 0 —> (3x – 4)(x – 1) ≤ 0
we get 1 and 4/3 as critical points. We place them on number line.

Since the number line is divided into three regions, now we can get 3 ranges of x
i) x < 1 (all values of x when substituted in (3x – 4)(x – 1) makes the product positive)
ii) 1 ≤ x ≤ 4/3 (all values of x when substituted in (3x – 4)(x – 1) makes the product negative)
iii) x > 4/3 (all values of x when substituted in (3x – 4)(x – 1) makes the product positive)
At this point we should understand that for the inequality (3x-4)(x-1) ≤ 0 to hold true, exactly one of (3x-4) and (x-1) should be negative and other one be positive. Let’s examine 3 possible ranges one by one.
i) If x > 4/3, obviously both the factors i.e. (3x-4) and (x-1) will be positive and in that case inequality would not hold true. So this cannot be the range of x.
ii) If x is between 1 and 4/3 both inclusive, (3x-4) will be negative or equal to zero and (x-1) will be positive or equal to zero. Hence with this range inequality holds true. Correct.
iii) If x < 1, both (3x-4) and (x-1) will be negative hence inequality will not hold true.
So the range of x that satisfies the inequality 3x^2 – 7x + 4 ≤ 0 is 1 ≤ x ≤ 4/3
The steps to solve a quadratic inequation are as follows:
- Isolate the variable and always keep the variable positive.
- Maintain the Inequation in the form ax^2 + bx + c > 0 or < 0.
- Obtain the factors of Inequation.
- Place them on number line. The number line will get divided into the three regions.
- Mark the rightmost region with + sign, the next region with a – sign and the third region with a + sign (alternating + and – starting from the rightmost region).
- If the Inequation is of the form ax^2 + bx + c < 0, the region having the – sign will be the solution of the given quadratic inequality.
- If the Inequation is of the form ax^2 + bx + c > 0, the region having the + sign will be the solutions of the given quadratic inequality.
Question: Will the above procedure hold good even for a cubic or a fourth degree equation?
Answer: YES. For a cubic inequality we get 3 critical points which when plotted on the number line divides the number line into 4 regions. Mark the rightmost region as +ve and alternate the sign as shown below

Now based on whether the right hand side of the cubic inequality is < 0 or > 0 we get the solution to lie in 2 of the 4 regions.
4. Quantitative Comparisons on the GRE
Now that we are through with the properties of inequalities, lets see how we can make use of these properties in quantitative comparisons.
A quantitative comparison question is a big inequality in itself since it asks you to compare and determine which of the two quantities is greater. So the rules of inequalities can be used here, provided the initial comparison is not tampered with.
For e.g. If we consider a basic quantitative comparison question where quantity B is clearly greater than quantity A,
Quantity A Quantity B
4 6
Adding 2, Quantity A becomes 6 and Quantity B becomes 8. Quantity B is still greater.
Subtracting 2, Quantity A becomes 2 and Quantity B becomes 4. Quantity B is still greater.
Multiplying by +2, Quantity A becomes 8 and Quantity B becomes 12. Quantity B is still greater.
Dividing by +2, Quantity A becomes 2 and Quantity B becomes 3. Quantity B is still greater.
Multiplying by -2, Quantity A becomes -8 and Quantity B becomes -12. Quantity A is greater.
Dividing by -2, Quantity A becomes -2 and Quantity B becomes -3. Quantity A is greater.
It is very evident that if we multiply or divide by a negative number the comparison will never be consistent with the initial comparison.
Points to Remember
Here are a few things you need to remember when you are using the properties of inequalities to simplify complex quantitative comparison questions:
1.Add or subtract any value to both quantities.
2.Multiply or divide by a positive value.
3.Square both sides only when the quantities are both positive.
4.Never multiply or divide both quantities by a negative number.
5.Never multiply or divide both quantities by a variable if the sign of the variable is unknown.
6.If the sign of the variable is always positive then it is possible to multiply or divide both quantities by the positive variable (for e.g. x2 ,since x2 is always positive).
After reading our simple guide, you should now know what strategies you must employ for inequality questions on the GRE!
We hope this guide helps you along the way to a 170 on GRE Quant!
