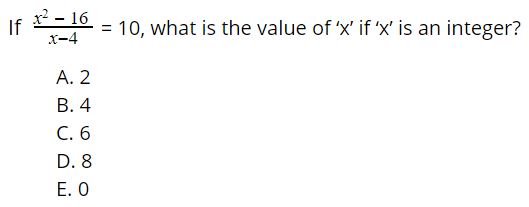“I love algebra! It’s so plain and simple!”
Said nobody, ever.
The mere idea of Algebra gave us nightmares when we were in school. Algebra was like a giant ‘x’ – full of random variables and symbols that we couldn’t make head or tail of!
However, you cannot hide behind excuses like how completely terrible you think Algebra is – if you want to get a 165+ in GRE Quant, that is.
Here’s the thing:
If you genuinely wish to up the ante, you cannot “not do well” in Algebra. You cannot say that you will try to cover it up in the other three sections.
So buckle up and let’s do this thing!
We’ll give you the lowdown on five basic tips to improve your performance in Algebra. By the time you finish reading this blog, you should have a fair idea of what you can do to score well in this area of GRE Quant.
Why is Algebra Important?
Before we answer that question, here’s an interesting fact about the origin of the word ‘algebra’. It comes from the Arabic term, ‘al-jabr’ which means the reunion of broken parts. How interesting, right?!
Questions based on Algebra account for around 15% to 20% of the questions in a GRE Quant section. So, this means you should expect 3 to 4 questions per section to be based on Algebra.
Hence, considering that there are either two or three Quant sections on the GRE, you should expect to see anywhere between 6 and 12 Algebra questions on one entire GRE test. That is a BIG chunk of the questions!
Further, GRE Quant Algebra covers 5 basic sub-categories:
- Linear & Simultaneous equations
- Quadratic equations
- Inequalities (Linear & Quadratic)
- Absolute values
- Functions
Of these, equations and inequalities get the highest weightage in terms of importance. Questions from functions and absolute values are relatively easier and fewer in number.
With this approximate picture in mind, let’s move on to exploring 5 super-useful tips to help you boost your GRE Quant score.
1. Start Out Positive
We cannot stress enough on the importance of starting out with a positive mindset about GRE Quant or even just algebra.
We know it is easier said than done, especially considering how much everyone seems to hate algebra.
And we know you’re probably thinking, “Dude, ‘positive’ is the last thing I can bring myself to feel about Algebra.” Trust us, we know the feeling. If you simply cannot feel positive about Algebra, try to at least develop a neutral perspective towards it.
Starting off with a negative attitude and thinking about all the horrible experiences you’ve shared with Algebra is the worst thing you could do for yourself right now. It just takes a few wrong answers for this feeling to spiral out of control and you will be back in familiar territory again cursing Algebra and saying “Algebra sucks, big time!”
And you’re not going to score a 165+ with that attitude.
Instead, if you start off by telling yourself, “Okay, let’s just give this a shot,” a few wrong answers will only end up fortifying your determination to get the next few questions right.
Every time you pick up the book to solve Algebra questions, remember that the only score you have to beat is your own previous score.
If you got 5 right answers out of 10 yesterday, all you have to do today is get 6 answers right instead.
This will help you stay calm and collected.
With a calm and collected mindset, you’ll be able to perform better on every consecutive question, too.
2. Get Equations and Inequalities Sorted
Having a good grasp of the basic concepts is fundamental to doing well in any area of study. It’s no different with Algebra.
If you want to be good at solving equations, you need to know some standard equations which are universally true.
Similarly, if you want to solve more inequality problems correctly, you need to be good at reproducing the basic concepts of inequalities.
Simple things are not so simple, because we usually undermine their importance.
For example, look at algebraic identities.
How many algebraic identities can you rattle out in under a minute?
We’re not kidding, this is dead serious! Try it! Here’s what we came up with:
1. (a+b)^2 = a^2 + b^2 + 2ab
2. (a-b)^2 = a^2 + b^2 – 2ab
3. a^2 – b^2 = (a+b) (a-b)
4. (a+b+c)^2 = a^2 + b^2 + c^2 + 2ab + 2bc + 2ac
5. (a+b)^3 = a^3 + b^3 + 3ab (a+b)
6. (a-b)^3 = a^3 – b^3 – 3ab (a-b)
7. a^3 – b^3 = (a-b) (a^2 + ab + b^2)
8. a^3 + b^3 = (a+b) (a^2 – ab + b^2)
Wondering how knowing a few equations will help you? Let’s take a sample question to help you figure that out. 🙂
Sample Question:
3. Don’t Solve Everything
No, we’re not out of our minds – hear us out!
We know it makes us sound cuckoo, advising you not to try and solve everything when solving stuff is literally all that’s expected of you.
But here’s the thing:
Solving is NOT what’s expected.
Think about it – GRE Quant is about finding the answer to every math question thrown your way, sure, but solving it is not the only way to find the answer!
Most of us work on a more or less ‘automatic’ mode when it comes to dealing with math. We just get into calculations without over-analyzing the given question. And that works out well most times.
However, that will work against you when it comes to GRE Quant.
While Math requires solving, the GRE test doesn’t provide enough time for you to actually do that every time. Remember, the GRE doesn’t care how you arrive at a solution, they only care about whether you get to the right one in time.
As we mentioned in our blog on GRE Quant, ‘Quant’ means much more than Math. Don’t approach it like Math.
Here’s what you can do instead of solving, from time to time:
Eliminate wrong answer options till you’re left with just one possible answer. Let’s consider an example to demonstrate this.
Sample Question:
Solve for the range of x : 16 + x > 8x – 12
A. x > 5
B. x > 10
C. x = 4
D. x > 4
E. x < 4
Solution:
You know the usual way of solving this inequality-based question. Let’s try it our way:
To begin eliminating the available answer choices, we always start by plugging Option C into the question.
In this case, Option C is x = 4. Plugging that into the inequality, we get:
LHS: 16 + 4 = 20
RHS: 32 – 12 = 20
In short, LHS = RHS. Given that this is supposed to be an inequality-based problem, Option C is clearly not the right answer.
As the next logical step, let’s try option D, which says x > 4. What’s the first number that comes to mind when you consider x > 4?
For us, it is 5. So, we’ll plug that in to see if it works, but you can choose whatever number you want.
With x > 4 (or x =5 in this case),
LHS: 16 + 5 = 21
RHS: 40 – 12 = 28
So, LHS < RHS. Meaning Option D is not the answer, either.
Consider this: if x > 4 gave us LHS < RHS, surely the values given in options A and B will also give us the same result. Thanks to this, we can not only eliminate option D, but also options A and B.
With A, B, C, and D, all eliminated, we’re only left with Option E, which HAS to be the answer.
Hope our little demo here has given you enough reason to believe that we’re not crazy and that solving everything is actually not necessary.
By the way, a word of caution here:
Don’t think that we are advocating the method of ‘trial and error’ as a substitute to conceptual depth. This trickery will only work with MCQs, and inequalities will appear on the test in all forms including quantitative comparison and numeric entry.
Sure, you should play smart wherever you can and reduce your workload, but rest assured, this cannot be done unless your basic concepts are clear.
4. Don’t Get Overwhelmed by Word Problems
By ‘word problems’, we mean those questions which have statements that look more like an AWA essay.
Sometimes, you wonder whether the problem is testing you on your knowledge of Math or Reading Comprehension!
Honestly, though, your RC skills are also being tested here. If you don’t manage to make sense of the question statements, you will end up messing up the equation and hence, the answer.
So, the best thing to do when you encounter highly verbose word problems is to keep calm and not get overwhelmed by the situation. Remind yourself that you have tackled RC passages in Verbal which had far greater verbiage.
Sounds logical, right?
The thing is this:
If you start freaking out because you can’t make sense of the question right away, you’ll lower your chances of figuring out what it means within the time limit you have. Besides, none of us is Shakespeare, we all have trouble with complicated language.
It’s okay if you don’t immediately understand. Take a moment, sip on some water and take a deep breath.
Remember this:
A lengthy word problem is like a Paper Masala Dosa. If you try eating it in one bite, you’re going to choke on it. So, take your time and eat your question masala dosa one bite at a time – interpret the word problem in parts, develop variables and then integrate the parts into a whole.
That actually brings us quite conveniently to the next part of this article!
5. How to Develop the Right Variables
In word problems on equations/inequations, you get the right answer only if you have framed the right equation/inequation.
Most of the time, people don’t have issues with solving equations – that’s the easy part. What’s difficult is developing equations/inequations from word problems. For those of you who just went, “YEAH DUDE!” in your heads, here are five simple steps to help you decode word problems into the appropriate math sums!
Step 1
Scan the entire question by quickly going through it to get a gist of what the question demands as an answer. Your sole aim here is to figure out what the question is asking, forget all the data it gives to help you do so.
Step 2
Map the important pieces of information from your first reading. This is the stage where you pay attention to the data provided in the question. When you do this, you’ll have a rough idea of what the variables could be and also what the required mathematical operations could be.
Step 3
Develop the variable/variables based on the mapping.
Step 4
Using the mathematical operations described in the statements, connect the variables and form an equation.
Step 5
Solve the equation.
The number of unknown factors generally represents the number of variables.
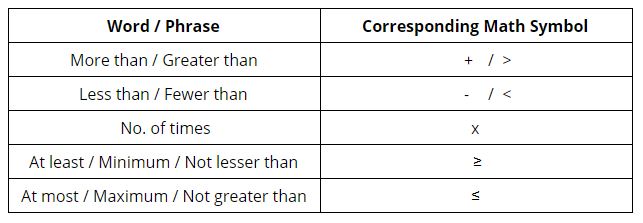
Words like more than, less than etc., represent specific mathematical operations which form the connections between the variables, represented using the symbols =, >, < , ≤, and ≥.
The following table is a ready reckoner to convert certain phrases into their mathematical counterparts:
Let’s look at a sample question to understand how this can be done.
Sample Question:
At a fruit stand, bananas can be purchased for $0.15 each and oranges for $0.20 each. At these rates, a bag of bananas and oranges were purchased for $3.80. If the bag contained 21 pieces of fruit, how many of the pieces were oranges?
A. 8
B. 10
C. 13
D. 15
E. 16
Solution:
The unknown values here are the number of bananas and the number of oranges. Hence, these are the variables which have to be assumed.
Let the number of bananas be ‘x’ and the number of oranges be ‘y’.
Here’s what we know:
Cost of each banana = $ 0.15 and the cost of each orange = $ 0.20.
If 1 banana costs $0.15, 2 bananas cost $0.30 i.e. 2 x $ 0.15. Right?
Applying a similar analogy, we can say that x bananas cost $0.15x and y oranges cost $0.20y. When we add these two individual costs, we arrive at the total cost. Combine this with what’s already given and this is what you get:
$0.15x + $0.20 y = $3.80
Since we have two variables, we need two independent equations in order to find unique values for each. It’s quite easy to obtain the second equation because we already know that there were 21 pieces of fruit in the bag. Mathematically, this is written as:
x + y = 21
What do we do next? If you answered “Solve both the equations”, then you have forgotten point #3 of this blog.
As mentioned before, we start by substituting Option C in both the equations and check if it works out. If it does, then that’s our answer.
Remember that we’re trying to calculate the number of oranges. So, the given answer options are talking about the variable ‘y’. As per Option C, y = 13; therefore, x = 8. Hence,
$0.15 x 8 = $1.20 and $0.20 x 13 = $2.60
$1.20 + $2.60 =$3.80
Well, what do you know! Both equations are satisfied if y = 13. Hence, option C is the right answer.
Conclusion
In conclusion, the idea is to keep your mind relaxed and be aware of everything you see on the question paper. This will help you with GRE Quant Algebra, Geometry, Arithmetic, as well as Data Interpretation.
So, that is about it, folks! We hope that you found this blog useful in your preparation for Quant on the GRE. We look forward to hearing from you about how you incorporated these techniques in your prep and how they helped you.