GRE quant arithmetic is often referred to as GRE math as well, which could be a good indication of why so many people are so intimidated by it. Fortunately, though, the truth is that GRE math is only a very small part of the mammoth subject of mathematics.
If you’re wondering what GRE quant tests, it’s just stuff we’ve learned in school.
Honestly! We’re not kidding.
However, we understand if you still have reservations in your mind about how easy GRE math really is. So, we’ve made a series of articles on the different parts of GRE quant with one article each on arithmetic, algebra, data interpretation, and geometry.
In this article, as the title suggests, we will focus on Arithmetic. Here’s what this article will talk about at length:
The word ‘arithmetic’ is derived from the Greek word, ‘arithmos’ which means number. Arithmetic is the branch of mathematics which deals with the study of numbers and their properties.
For a fairly long time in the history of mathematics, arithmetic has been synonymous with number theory. However, when we approach Arithmetic from a Test Prep perspective, we can see it in a much broader sense.
Arithmetic on GRE Quant
Generally, arithmetic refers not only to Number Theory but also to its various applications including ratios and percentages and their respective applications, too.
As such, arithmetic is indeed the Queen of Math, especially when it comes to the GRE, because it constitutes almost 50% of the questions in the Quant section.
Questions from GRE Quant Arithmetic basically boil down to Number Theory, Ratios, Percentages, or Application-Based Topics.
Therefore, preparing for arithmetic entails preparation on these topics.
Let’s now look at each of these topics in detail, beginning with Number Theory.
1. Number Theory
One of the greatest mathematicians of all time, Carl Friedrich Gauss, once said,
“Mathematics is the queen of the sciences and number theory is the queen of mathematics.”
Since Number Theory is the root of all numbers and mathematics is nothing but numbers, it’s only right that it should be considered the most important part of mathematics. As such, Number Theory is the study of different types of numbers and their properties.
Additionally, Number Theory is also a study of the behavior of various types of numbers when mathematical operations like addition, subtraction, multiplication, division, and exponentiation are performed on them.
For the sake of GRE Quant, topics under Number Theory can be broadly divided into the following categories:
1. Properties of Integers
2. Properties of Fractions
3. Exponents & Roots
Let’s dive into what questions each of these categories could throw up.
a. Properties of Integers
This is probably the broadest of all categories under Number Theory. Here are some concepts you might be tested on:
– Basic properties of different types of numbers (For example, Natural Numbers, Whole Numbers, Prime Numbers)
– Division Algorithm and Divisibility Rules
– Factors & Multiples with special emphasis on HCF and LCM
– Composite Number Concepts
– Remainder Concepts
– Factorial Notation
Sample Question:
If a number has a remainder of 4 upon division by 5 and a remainder of 2 upon division by 3, what remainder must it have upon division by 15?
i. 5
ii. 7
iii. 9
iv. 11
v. 14
Solution:
The basic equation for division is Dividend = Divisor x Quotient + Remainder.
Accordingly, a number which has a remainder of 4 when divided by 5 can be written in the form of 5k + 4, where k is the quotient and can take values of 0,1,2,3 and so on.
Hence, the possible values for the number are 4,9,14,19 and so on.
Further, a number which has a remainder of 2 when divided by 3 can be written in the form of 3p + 2, where p is the quotient and can take values of 0,1,2,3, and so on.
Hence, the possible values for the number here are 2, 5, 8, 11, 14 and so on.
So, when we look at both the lists of possible answers, we find that the common number in both sequences is 14. Thus, we can conclude that this is the number we are looking for.
As a rule, if a smaller number is divided by a larger number, the remainder is the smaller number itself. So, when 14 is divided by 15, the remainder is 14 itself.
Hence, the correct answer is option E.
b. Properties of Fractions
This part of Number Theory tests your knowledge of fractions and decimals, which are also referred to as Real Numbers.
The inherent nature of questions on fractions and decimals is that they consume a lot of time for even basic calculations. You have to be super sorted with the basic concepts here because if you’re not, you risk losing out on time.
Under this topic, you can expect questions from:
– Comparison of fractions
– Conversion of decimals to fractions
– Identifying whether a fraction represents a terminating decimal or a recurring decimal
Sample Question:
Which is greater, 17/21 or 21/25?
Solution:
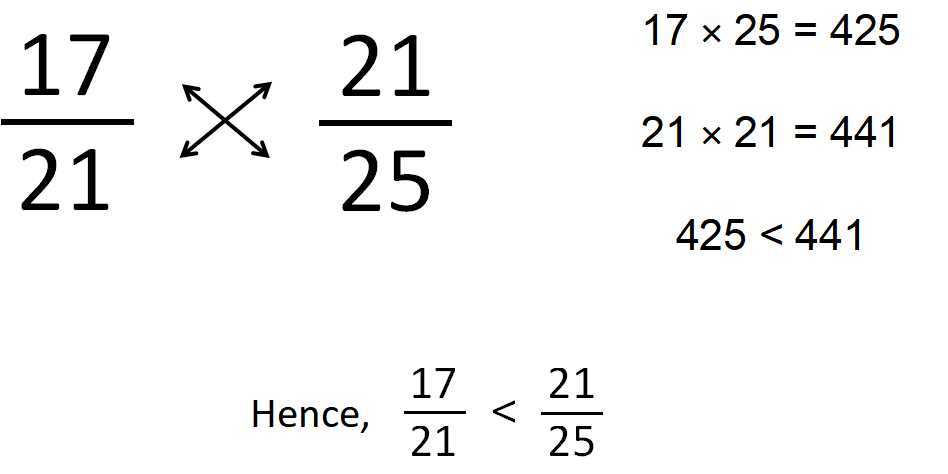
To compare fractions, cross multiply the numerator of the first fraction with the denominator of the second fraction and vice versa. The fraction on the side of the bigger product is the bigger fraction.
c. Exponents & Roots
This part of number theory tests your knowledge of exponents/indices and their rules. Questions from this area can include:
– Questions based on laws of indices
– Questions on cyclicity of units digit
– Maximum power of an integer in a factorial
Sample Question:
Find the units digit of 9^8235!
Ans: _____
Solution:
Any power of 9 always ends with a 9 or 1. Whenever 9 is raised to an odd power, the units digit of the resultant number is 9 and whenever it is raised to an even power, the units digit of the resultant number is 1.
Any factorial greater than 2 will always be an even number.
Hence, 8235! will be an even number.
Therefore, the question given to us can be written as 9even which will have a units digit of 1.
2. Ratios
Ratios are important not only because they can give direct problems but also because they are applied in other areas as well. You are expected to know the basic concepts of ratios so that you can apply them.
In this topic, you will be expected to solve problems on:
a. Interpreting ratios
b. Bridging ratios
c. Conducting mathematical operations on ratios
d. Word problems based on ratios
Sample Problem:
In a class of 35 students, if boys and girls are in the ratio of 2:3, how many girls are there?
Ans: _____
Solution:
Given that the ratio of boys and girls is 2:3. This means that for every 2 boys there are 3 girls.
Let the number of boys = 2x and the number of girls = 3x.
Then, 2x + 3x = 35
i.e. 5x = 35
Therefore, x = 7
Therefore, the number of girls which is 3x, will be 21.
3. Percentages
This is a very important topic because you’ll get direct questions related to it and you’ll probably also get questions related to its applications.
You can expect one or two direct questions on percentage concepts. However, the applications of percentages like Profit and Loss will also give you two to three questions.
Hence, the topic of percentages accounts for almost 40% of the Arithmetic questions. So, make sure that you are well prepared on this topic.
Direct questions on percentages could be based on
a. Basic percentage calculations
b. Percentage Change concepts
c. Successive percentage change concept
We will have a look at the application areas of percentages in the next section.
Sample question:
The price of a ticket increased from $80 to $84. Find the percentage increase in the price of the ticket?
Solution:
The percentage increase in a quantity is given by the expression:
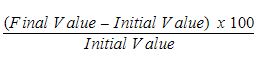
In this case, the initial value is 80 and the final value is 84. Substituting these values in the expression given above, we get 5% as the answer.
The value 5 has to be filled in the answer box provided.
4. Application-based topics
Application-based topics cover a large variety of sub-categories. The ones you could be tested on are:
a. Profit & Loss and Interest which are applications of Percentages
b. Word problems based on ratio concepts
c. Word problems based on number theory
d. Time & Distance and Time & Work which are applications of Ratios
a. Profit & Loss and Interest
Questions on Profit & Loss and Interest are usually perceived by students to be formula oriented topics. This means that you may have a stereotype in your head that you need to memorize a number of equations to be able to solve questions from these areas.
However, this is farthest from the truth. And the truth is that if you are well versed with the basic percentage calculations and percentage change concepts, Profit & Loss and Interest problems are mere applications of these concepts.
Hence, our advice to you would be to practice as many questions as possible from the Percentages topic so that you have built up sufficient muscle memory to tackle questions from Profit & Loss and Interest.
Sample Question:
A shopkeeper bought a pound of almonds at $4. He made a profit of 33.33% after giving a discount of 33.33%. Find the marked price of the pound of almonds.
i. $5
ii. $5.66
iii. $7
iv. $8
v. $9
Solution:
The cost incurred by the shopkeeper to purchase the almonds is $4. Hence, CP = $4.
If he made a profit of 33.33%, it means he made a profit of 4/3 (because 33.33% = ⅓ and remember, profit percentage is always calculated with reference to CP).
But, Profit = SP – CP
Hence, SP = CP + Profit
Therefore, SP = 4 + (4/3)
SP = 16/3
We know that he gave a 33.33% discount. Percentage of discount is always calculated with reference to Marked Price (MP). Let MP = x.
Then, Discount = x/3 (remember 33.33% = ⅓)
Discount = MP – SP
(x/3) = x – (16/3)
To simplify, we have x = 8.
Hence, the correct answer option is D.
b.Word problems based on ratio concepts
Word problems based on ratio concepts usually require you to apply the concept of interpreting a ratio and then build a mathematical version of the statements to solve the question.
Since a word problem is usually built around lengthy and complex statements, word problems also test your reading and comprehension skills.
They also test your ability to integrate different bits of data into a whole similar to solving a jigsaw puzzle.
Word problems based on ratios can be:
a. Word problems on interpreting ratios
b. Problems on ages
c. Problems on numbers and digits
Sample Problem:
Six years ago, the ratio of ages of Bob and Joe is 2 : 5. Four years from now, the ratio of their ages will be 4 : 5. Find the sum of their present ages.
Ans: _____
Solution:
Let the ages of Bob and Joe, six years ago, be 2x and 5x respectively.
Then, their ages, four years from now, will be 2x + 10 and 5x + 10 respectively.
It is given that the ratio of their ages, four years from now is 4:5.
Therefore, 2x + 105x + 10 = 45
Solving this, x = 1.
Therefore, the present ages of Bob and Joe are 2 and 5 respectively which means the sum of their present ages is 7.
c. Word problems based on Number Theory
Word problems based on number theory also test your comprehension and interpretation skills. Along with these, they also test your in-depth knowledge of number theory concepts.
Word problems on number theory are usually based on properties of numbers.
Sample Question:
Sum of the LCM and HCF of two numbers is 760, and LCM is 18 times their HCF. If one number is 360, then the other number is:
i. 20
ii. 48
iii. 64
iv. 80
v. 96
Solution:
Let the two numbers be x and y; let their HCF be H and their LCM be L.
Then, L + H = 760
It’s also given that L = 18H.
Substituting this in the equation above, we have 18H + H = 760
Therefore, 19 H = 760 or H = 40.
Hence, L = 18 x 40 = 720.
Let x = 360.
Product of two numbers = Product of their HCF and LCM.
Therefore, 360 x y = 40 x 720
Therefore, y = 80.
So, the correct answer is Option D.
d. Time & Distance and Time & Work
Both the topics mentioned above are the most significant applications of all topics that you learn in Arithmetic namely Numbers, Ratios and Percentages.
This is because questions from these two areas usually involve multiple concepts drawn from multiple topics, intertwined in such a way that a person without a firm grasp of all the concepts will find the going tough.
This is also the reason why these two topics contribute at least 3 to 4 questions to the Quant section.
Sample Question:
Stan drives at an average speed of 60 miles per hour from Town A to Town B, a distance of 150 miles. Ollie drives at an average speed of 50 miles per hour from Town C to Town B, a distance of 120 miles.
|
Quantity A |
Quantity B |
|
Amount of time Stan spends driving |
Amount of time Ollie spends driving |
Solution:
Speed = Distance/Time
Hence, Time = Distance/Speed
Stan’s Speed is 60 mph and he has covered a distance of 150 miles. Hence, the time taken is (5/2) i.e. 2.5 hours.
Similarly, the time taken by Ollie is (12/5) i.e. 2.4 hours.
Hence, Quantity A is definitely greater than Quantity B.
The correct answer option is Option A.
Conclusion
So, that is all for now, folks! This is everything we thought you might need some clarity on for now.
With this blog, we hope we have given you enough ammunition to ruminate on and plan your prep for Arithmetic.
Go ahead, pick up that study material and get cracking with your GRE Quant prep!
