Does the very idea of GRE Quant give you the jitters?
Are multiple sources of information confusing you further rather than helping you understand GRE quant?
Would you like to take advantage of the GRE exam pattern to target a 165+ score on quant?
If you answered with a ‘No’, we’re happy to see that you have your GRE math act together! Congratulations, well done! We do hope that this article will help you anyway.
If you answered these questions with a “YES!”, look no further. You have come to the perfect place!
In this blog, we’ll be giving you a detailed insight into the Quantitative Reasoning (QR) section of the GRE. Here’s a quick roadmap to help you navigate this article.
- GRE Test Pattern
- Scoring Pattern for GRE Quant
- Quant vs Math
- Subsections in GRE Quant
- Using the Calculator
Let’s begin by refreshing our knowledge of the GRE test pattern.
GRE Test Pattern
Here’s what the GRE pattern looks like:
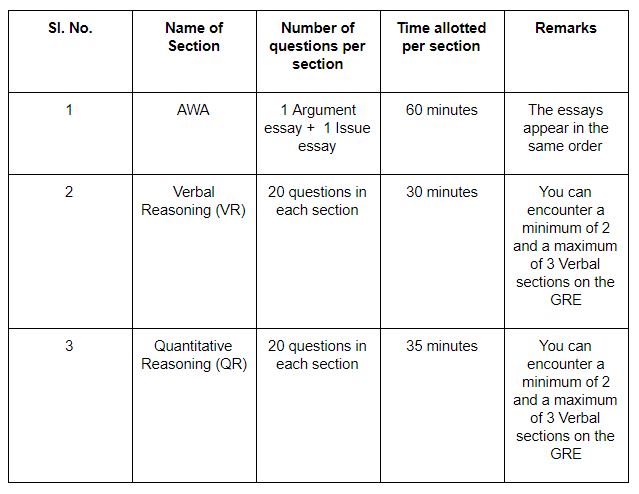
The test starts off with the mandatory AWA section which spans the first 60 minutes.
Next, you’ll either get a Quant section or a Verbal section to solve, but which one comes first is decided at random. Based on which section comes first, you can figure out how many of which section you should expect.
If your AWA is followed immediately by a VR section, it means that you will see 3 VR sections interspersed by 2 QR sections. However, if you see a QR section following your AWA section, it means you will be required to answer 3 QR sections and 2 VR sections.
Whichever way it is, you are required to answer 100 questions (20 questions per section x 5 sections) in 160 minutes to 165 minutes.
This is because one of the five sections is an unidentified experimental section, which will not be scored.
However, since it is an unidentified section, we advise you to go ahead and answer the test as though it actually contained 100 questions.
Scoring Pattern for GRE Quant
Your performance on the two scored sections of GRE math is first converted to a raw score. This raw score is based on how many questions you answered right and how many you answered wrong.
This raw score is then converted to a scaled score which can range from 130 to 170, in single-point increments. So, even if you get all the Quant questions wrong, you will still get a 130. But that’s the equivalent to getting a zero on GRE quant.
Statistically, scoring 165 on GRE math represents the 89th percentile.
This means that if you get 165, you have scored as much as or more than 89% of all the GRE test takers. In other words, you are in the top 11 percent of all students who took the GRE.
Food for thought – The highest score one can get in Quant is 170, which represents the 100th percentile. This is a difference of just five points in terms of marks scored, but when it comes to percentiles, the same distance represents an 11-point difference. What does this tell you?
The only reason this can happen is that a substantial number of people get scores between 165 and 170. What does THIS tell you?
In our opinion, this suggests that it’s not all that difficult to get that perfect GRE quant score.
So! Let’s now get into dissecting GRE quant so that you have a very clear understanding of the whole thing by the time you finish reading this blog.
Quant vs. Math
You may notice that the words ‘quant’ and ‘math’ are used interchangeably, even in this blog.
However, here’s the thing:
Quant ≠ Math. At least not on the GRE.
Mathematics is akin to outer space, in that it is MASSIVE. You could go from school level mathematics to post-doctoral degree-level math and still not cover everything there is to know about mathematics. There’s literally nothing in the universe that is unrelated to math.
Seriously, if you have doubts or think this is crazy-talk, Google ‘golden ratio‘. Oh and also, just for fun (yes, fun) try this website out.
Mathematics is not only about formulae; it is also about theories, theorems, propositions, proofs, and a whole bunch of other things that are difficult to comprehend, even for the best of us.
The point is, it’s a capital mistake to mix up quant and math in your head. You’ll just end up making a mountain out of a molehill because the GRE quant is only a very small subset of the gigantic subject called Mathematics.
Quantitative Reasoning on the GRE is exactly like it sounds. It looks to gauge your reasoning skills – both analytical and logical – when it comes to numbers, along with your basic mathematical skills.
When we say ‘basic mathematical skills’, we mean the fundamental level of mathematics we all learned in high school, regardless of how our academic paths digressed from there on.
Didn’t we all learn that the sum of the three angles in a triangle is 180 degrees?
This is an example of a basic mathematical skill we all acquired when throughout our school lives. In GRE math, this is the level that you’re expected to be well-versed with.
As a rule, the GRE doesn’t look to find mathematicians. The objective is to test intelligence, which mostly means the ability to apply whatever you do know. GRE quant measures your ability to estimate, use logic, use the given answer options and eliminate them to solve the questions you face – in short, your ability to use ‘reasoning’ with numbers.
We hope that this has assuaged at least some of the fears and mental blocks you may have had with respect to GRE math/quant. Please note that we only mean a small subset of mathematics when we say ‘GRE math’ or ‘GRE quant’, and not the entire mammoth that is math.
Next, we talk about what actually constitutes ‘GRE quant’.
Subsections in GRE Quant
There are three ways in which you can divide GRE Quant to help you study it properly.
Let’s get into the details of each of these, one at a time.
I. Based on Areas of Math
The questions in GRE quant comprise of questions drawn from the following areas of Math:
1. Arithmetic
2. Algebra
3. Geometry
4. Data Analysis
Of these, Arithmetic takes the lion’s share of importance – almost 8 to 10 out of 20 questions come from Arithmetic. That’s almost 50%, which is why preparing well for Arithmetic questions is of paramount importance.
Algebra and Data Analysis each account for 15% to 20% of the questions, while Geometry accounts for 10% to 20% of the questions.
As we said before, the questions you can expect from each of the four areas will be from topics that you learned in high school. But, this is not to say that you will be tested on all the topics that you learned in high school.
Topics like Logarithms, Progressions, Relations and even Trigonometry are not tested on the GRE.
Relieved to hear that? We know the feeling!
II. Based on Question Types
There is another way of categorizing Quant questions – it’s based on question types. There are four different types of questions in GRE Quant which you need to be aware of. They are:
1. Quantitative Comparison
2. Multiple Choice – Select One Answer Choice
3. Multiple Choice – Select One or More Answer Choices
4. Numeric Entry
Now, let’s examine each one of these in further detail.
1. Quantitative Comparison (QC)
Although this type of question tests your basic mathematical skills, it tests your reasoning and estimation skills to a larger extent. The basic structure of a Quantitative Comparison question is shown below:
Information / Constraints
|
Quantity A |
Quantity B |
A. Quantity A is greater
B. Quantity B is greater
C. The two quantities are equal
D. The relationship cannot be determined from the information given.
As you can see, QC questions test your ability to compare two quantities and arrive at a conclusion about their magnitude. Generally, 6 to 8 out of 20 questions will be QC questions.
This goes to show the importance that this question type holds in GRE Quant.
A QC question may have additional information/constraints given above the two quantities or may not have. Based on this, you are required to compare the two quantities and mark the relevant options out of the four.
Accordingly, you will mark:
Option A if Quantity A is ALWAYS greater than Quantity B.
Option B if Quantity B is ALWAYS greater than Quantity A.
Option C if Quantity A is ALWAYS equal to Quantity B.
Option D if a definite relationship cannot be established between the two on the basis of the information provided.
The pertinent point to be noted here is the word ALWAYS.
For example, if Quantity A is sometimes greater than Quantity B but sometimes lesser than Quantity B, then Option A cannot be marked as the answer. Similar reasoning can be applied to the other options as well.
Sample Question:
Akshay is younger than Chitra
|
Twice Akshay’s Age |
Chitra’s age |
A. Quantity A is greater
B. Quantity B is greater
C. The two quantities are equal
D. The relationship cannot be determined from the information given
Now, if you observe this question, there is hardly any math involved in solving this question except basic inequality concepts.
Consider Akshay’s age = 10 and Chitra’s age = 20; in this case, Quantity A will be equal to Quantity B.
On the other hand, consider Akshay’s age = 10 and Chitra’s age = 30; in this case, Quantity A will be lesser than Quantity B.
Since we are unable to say whether Quantity A is ALWAYS equal to B or ALWAYS less than B, the answer to this question is option D.
2. Multiple Choice – Select One Answer Choice
This question type is something most of us will be familiar with. In this question type, a question will be followed by five answer options named A, B, C, D and E. Your job is to solve the question and pick one of the five options, which you think is the answer.
Two points to note about this question type:
– There is one and only one correct answer to each question.
– The five options will be arranged in either ascending order or descending order of magnitude if numbers constitute the options.
While solving questions of this type, you need to make use of point number 2 above, by eliminating options and retaining those which you think could make the cut.
If you resort to the conventional methods in all problems of this type, you will end up wasting precious time whilst getting the same answer which does not sound commonsensical.
Approximately 6 to 8 questions of this type can appear in the Quant section. Therefore, this question type coupled with QC constitutes almost 75% of the entire Quant section of the GRE.
Sample Question:
Which of the following numbers is the farthest from the number 1 on the number line?
A. -10
B. -5
C. 0
D. 5
E. 10

From the given diagram, it is clear that -10 is the farthest number from the number ‘1’. Hence, Option A is the correct answer.
3. Multiple Choice – Select One or More Answer Choices
This is the more challenging variant of the Multiple Choice question type. Here, a question can be followed by any number of answer options ranging from 3 to 10 and therein lies the challenge. Your job is to select all the answer choices applicable under the conditions given.
A few points to note about this question type:
– These questions are marked with square boxes beside the options, not circles or ovals.
– Some questions of this type might ask you to mark a specific number of options as answers.
– Some other questions of this type might ask you to mark all those options as answers as are applicable.
– Some questions of this type might also have only one correct answer.
– No partial credit is awarded ( in this sense, this question type is analogous to the multiple blank questions that you encounter in SE or TC of the Verbal section of the GRE).
Eliminating as many options as possible by logic and estimation is a very good strategy to adopt in such questions. Elimination based on concepts is also a good method. Plugging in the remaining options into the question and checking if all of them apply, is the last stage of filtration before finalizing the answer options.
Around 3 to 4 questions in the Quant section belong to this question type. Hence, this question type does not pose that big a challenge anyway.
Sample Question:
Which of the following integers are multiples of both 2 and 3? A. 8 B. 9 C. 12 D. 18 E. 21 F. 36
This is a very simple question based on divisibility concepts.
Any number that is a multiple of 2, is an even number. So, if a number has to be a multiple of both 2 and 3, it has to be an even number first.
Based on this, we can eliminate options B and E, since they are not even.
Now, the next step is to eliminate the numbers which are not multiples of 3. Clearly, 8 is not a multiple of 3. Hence, Option A can be eliminated.
We are left with options C, D and F. Let us see if these are the final options which we can retain.
Any number which is a multiple of both 2 and 3 is a multiple of 6. All three numbers, i.e., 12, 18 and 36 are DEFINITELY multiples of 6. Hence, we can retain options C, D and F as the final answer.
There we go: the correct options to be marked are C, D, and F!
4. Numeric Entry
This is probably the only question type that we can all relate to from our school days. Because this is the question type where you have to work out the problem from start to end and there are no options provided!
Yep, you read it right!
No options are provided as part of the question. So, you have to be extra careful while reading and analyzing the question and working it out methodically.
You will be required to type in your answer in a single box if your answer is an integer or a decimal, or in two boxes if your answer is a fraction.
The good news is that this question type contributes a measly 10% of the total number of questions in Quant. So you may expect 1 or 2 questions from this type.
A few points to note about the Numeric Entry question type:
– Sometimes, there will be labels before or after the answer box to indicate the appropriate type of answer.
– If you are asked to round the answer, make sure you round it to the required degree of accuracy.
– Only mark the final answer in the box and not any of the intermediate answers that may be a part of your solution.
– Enter your answer as an integer or a decimal if there is a single answer box OR as a fraction if there are two separate boxes—one for the numerator and one for the Denominator.
– To enter an integer or a decimal, either type the number in the answer box using the keyboard or use the Transfer Display button on the calculator.
i. First, click on the answer box—a cursor will appear in the box—and then type the Number.
ii. To erase a number, use the Backspace key.
iii. For a negative sign, type a hyphen. For a decimal point, type a period.
iv. To remove a negative sign, type the hyphen again and it will disappear; the number will remain.
v. The Transfer Display button on the calculator will transfer the calculator display to the answer box.
vi. Equivalent forms of the correct answer, such as 2.5 and 2.50, are all correct.
vii. Enter the exact answer unless the question asks you to round your answer.
– To enter a fraction, type the numerator and the denominator in the respective boxes using the keyboard.
i. For a negative sign, type a hyphen. A decimal point cannot be used in the fraction.
ii. The Transfer Display button on the calculator cannot be used for a fraction.
iii. Fractions do not need to be reduced to lowest terms, though you may need to reduce your fraction to fit in the boxes.
Sample Question:
A rectangle R1 has a length of 25 and a width of 20, while another rectangle R2 has a length of 30 and a width of 20. What is the ratio of the perimeters of the two rectangles?

The perimeter of a rectangle is given by the formula 2 (l+b) where ‘l’ represents the length of the rectangle and ‘b’ represents the breadth/width of the rectangle.
Therefore:
Perimeter of R1 = 2(25 + 20) = 2(45) = 90
Perimeter of R2 = 2(30 + 20) = 2(50) = 100
Hence, the required ratio is 9:10. Remember that, because the question is asking you to find out a ratio, you have to simplify it to the lowest form before entering the numbers 9 and 10.
On the contrary, had the question asked you what fraction of perimeter of R2 is perimeter of R1, then you could directly plug in 90 and 100 without worrying about simplifying it to the lowest form.
III. Based on the Relevance of the Question
The two question types based on the relevance of a Maths question are:
1. GRE Quant Questions Described in a Real-Life Setting
Questions of this type are Maths questions where real-life scenarios are simulated/described in the questions.
Questions from Numbers, Word Problems, Time and Work, Time and Distance, Permutations and Combinations, Probability, Statistics & Data Interpretation, will all come under this category.
2. GRE Quant Questions Described in a Purely Mathematical Setting
Questions of this type are mostly concept-oriented and you may not be able to relate the situation described in the question to real life every time.
Questions from equations, inequalities, modulus, functions, and geometry, all come under this category.
Using the Calculator
The GRE proves to be a very student friendly test. This is testified by the fact that there is an onscreen calculator available for use in the Quant section.

Although you may think that using the calculator extensively will reduce the burden of calculations, it will actually do the opposite because you will end up spending a lot of time keying in the values.
Even if you make one error while keying in the values, you may end up getting a wrong answer, but you will not realize this until later, since you would not consciously notice that you made an error, because of the time constraints.
As such, our advice to you on using the calculator would be to use it:
1. When you are adding, subtracting, multiplying or dividing substantially large numbers so as to save time and improve accuracy;
2. When you are dealing with addition, subtraction, multiplication or division of decimals
3. When you have to find the square of a number which has 3 digits or more.
4. When your calculations involve finding a square root of a large perfect square or smaller imperfect squares
5. When estimation/approximation cannot be resorted to, to get to the answer.
On the other hand, avoid using the calculator for:
- Simple calculations, which you know can be done mentally.
- Questions where a fraction is required as an answer.
While using the calculator, make sure that:
- You do not mis-key the numbers or the signs.
- You know that all of the calculator’s buttons include Transfer Display
- You know that the Transfer Display function can be used only with Numeric Entry questions with a single answer box
- The calculator follows the PEMDAS sequence of operations while computing values
- The calculator gives an error for mathematical operations like Division by ZERO and the square roots of negative numbers.
We hope that we have given you all that you needed to know about the Quant section of the GRE.
We also hope that we have imbued you with a sense of confidence to take the Quant section head on and quell the challenge. So, go ahead and start preparing for the Quant section using some of the best resources you can find for GRE preparation, from CrackVerbal.
How did you find this blog on GRE Quant? Please let us know in the comments section below!