Solutions
Get detailed explanations to advanced GMAT questions.
Question
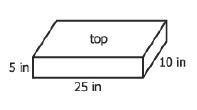
The outside of the rectangular box represented in the figure above is to be decorated by attaching pieces of wrapping paper to cover all surfaces except the bottom of the box. What is the minimum number of square inches of wrapping paper needed?
Option A:
375
Option B:
600
Option C:
725
Option D:
800
Option E:
1250
Difficulty Level
EasySolution
Option B is the correct answer.
Option Analysis
Total area of cuboid – area of bottom of cuboid = paper required to wrap all sides except bottom of the cuboid
Total area of cuboid = area of top and bottom side faces (l*b)+area of two side faces(h*b) + area of two side faces (l*h) = 2*25*10 + 2*5*10 + 2*25*5 = 500+100+250=850
Area of bottom face = 250
So paper needed = 850 – 250 = 600 square inches.
Related Questions
- The logo of a certain corporation is in the shape of a polygon, where all angles of a the polygon have…
- Relative to a group of other airlines, and airline’s degree of competition, c. for daily flights from City X to Destination Y…
- The cost of a certain phone call was $0.75 for the first 3 minutes and $0.20 for each additional minute…
- In a certain downtown office, 40 percent of the workers are men and 60 percent are women…
- P, Q, R and S are points on the number line in that order. If the distance from P to S is 10, what is the…